رگرسیون خطی در یادگیری ماشین Linear Regression

رگرسیون خطی یک روش آماری است که برای مدل‌سازی رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل استفاده می‌شود. این روش بینش‌های ارزشمندی برای پیش‌بینی و تحلیل داده‌ها فراهم می‌آورد. این مقاله به بررسی انواع، فرضیات، پیاده‌سازی، مزایا و معیارهای ارزیابی رگرسیون خطی می‌پردازد.

درک رگرسیون خطی

رگرسیون خطی همچنین یک نوع الگوریتم یادگیری نظارت‌شده در یادگیری ماشین است که از داده‌های برچسب‌خورده یاد می‌گیرد و داده‌ها را با توابع خطی بهینه‌شده‌ای تطبیق می‌دهد که می‌توان از آن‌ها برای پیش‌بینی داده‌های جدید استفاده کرد. این الگوریتم رابطه خطی بین متغیر وابسته و یک یا چند ویژگی مستقل را از طریق تطبیق یک معادله خطی با داده‌های مشاهده‌شده محاسبه می‌کند. این الگوریتم متغیرهای خروجی پیوسته را بر اساس متغیر ورودی مستقل پیش‌بینی می‌کند.

برای مثال، اگر بخواهیم قیمت خانه را پیش‌بینی کنیم، عواملی مانند سن خانه، فاصله از جاده اصلی، موقعیت، مساحت و تعداد اتاق‌ها را در نظر می‌گیریم. رگرسیون خطی از تمام این پارامترها برای پیش‌بینی قیمت خانه استفاده می‌کند زیرا رابطه خطی بین این ویژگی‌ها و قیمت خانه در نظر گرفته می‌شود.

چرا رگرسیون خطی مهم است؟

قابلیت تفسیر رگرسیون خطی یکی از بزرگ‌ترین نقاط قوت آن است. معادله مدل ضرایب روشنی را ارائه می‌دهد که تأثیر هر متغیر مستقل بر متغیر وابسته را نشان می‌دهد و درک ما از روابط زیرین را افزایش می‌دهد. سادگی آن یک مزیت بزرگ است؛ رگرسیون خطی شفاف است، پیاده‌سازی آن آسان است و به‌عنوان یک مفهوم بنیادین برای الگوریتم‌های پیشرفته‌تر عمل می‌کند.

حالا که توضیح دادیم چرا رگرسیون خطی مهم است، به نحوه کارکرد آن بر اساس خط بهترین تطبیق در رگرسیون می‌پردازیم.

خط بهترین تطبیق چیست؟

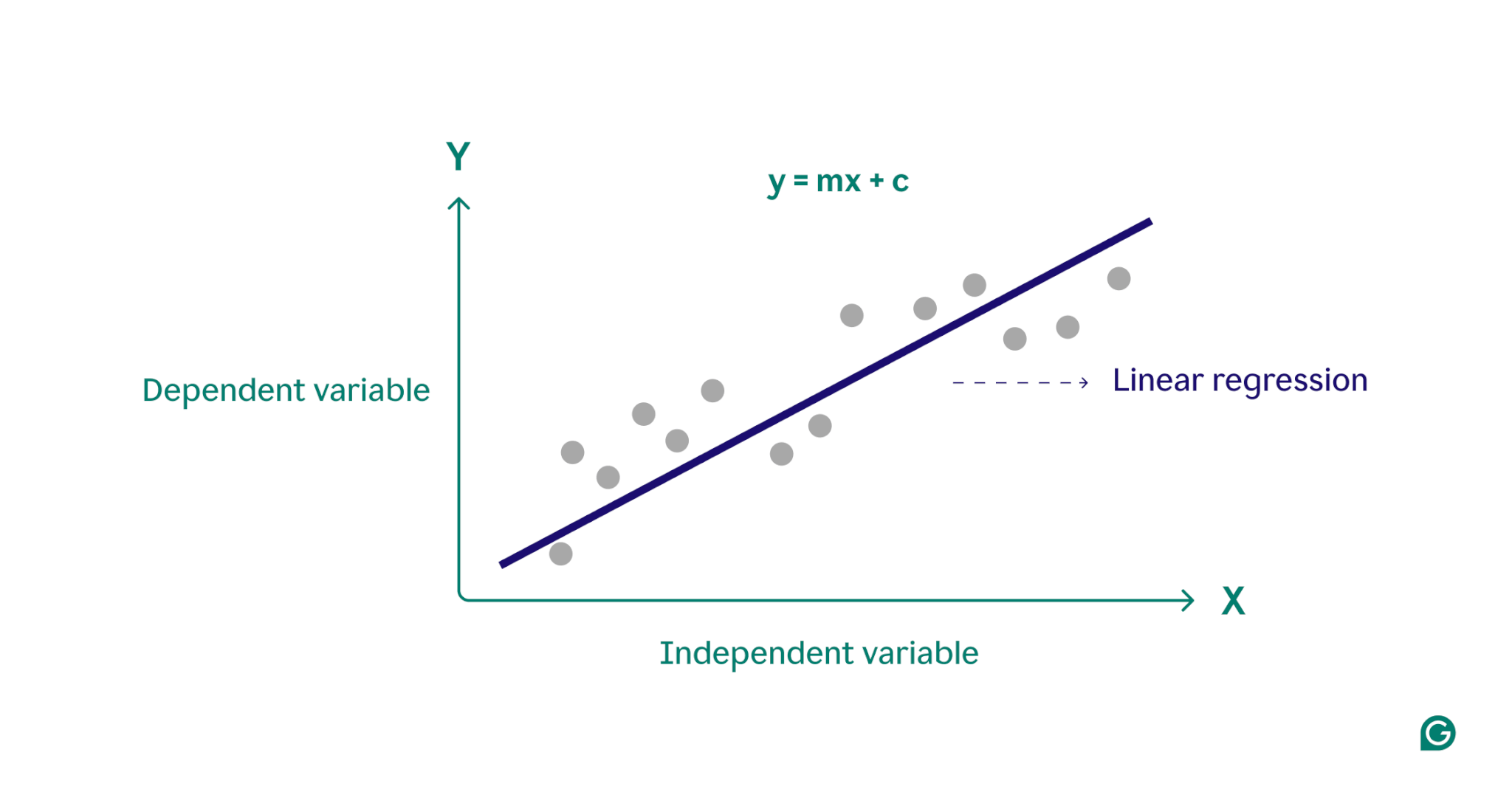
هدف اصلی در استفاده از رگرسیون خطی، یافتن خط بهترین تطبیق است که به این معنی است که خطا بین مقادیر پیش‌بینی‌شده و مقادیر واقعی باید به حداقل برسد. خط بهترین تطبیق کمترین خطا را دارد.

معادله خط بهترین تطبیق یک خط مستقیم است که رابطه بین متغیر وابسته و متغیرهای مستقل را نمایش می‌دهد. شیب خط نشان‌دهنده این است که متغیر وابسته چقدر به ازای یک تغییر واحد در متغیر مستقل تغییر می‌کند.

رگرسیون خطی در یادگیری ماشین

در اینجا Y به‌عنوان متغیر وابسته یا هدف شناخته می‌شود و X به‌عنوان متغیر مستقل یا پیش‌بینی‌کننده Y شناخته می‌شود. بسیاری از انواع توابع یا ماژول‌ها وجود دارند که می‌توانند برای رگرسیون استفاده شوند. تابع خطی ساده‌ترین نوع تابع است. در اینجا، X ممکن است یک ویژگی واحد یا چندین ویژگی باشد که مسئله را نمایندگی می‌کند.

رگرسیون خطی وظیفه پیش‌بینی مقدار یک متغیر وابسته (y) بر اساس متغیر مستقل داده‌شده (x) را انجام می‌دهد. بنابراین، نام آن رگرسیون خطی است. در شکل بالا، X (ورودی) تجربه کاری است و Y (خروجی) حقوق یک فرد است. خط رگرسیون خط بهترین تطبیق برای مدل ما است.

در رگرسیون خطی فرضیاتی برای اطمینان از قابلیت اعتماد نتایج مدل انجام می‌شود.

فرضیه در رگرسیون خطی

فرضیات عبارتند از:

خطیت: فرض می‌شود که رابطه‌ای خطی بین متغیرهای مستقل و وابسته وجود دارد. این بدان معناست که تغییرات در متغیر مستقل منجر به تغییرات متناسب در متغیر وابسته می‌شود.
استقلال: مشاهدات باید از یکدیگر مستقل باشند، به این معنی که خطاهای یک مشاهده نباید بر سایر مشاهدات تأثیر بگذارد.

همان‌طور که گفته شد، ویژگی مستقل ما تجربه کاری است یعنی X و حقوق مربوطه Y متغیر وابسته است. فرض می‌کنیم که رابطه‌ای خطی بین X و Y وجود دارد، سپس حقوق می‌تواند با استفاده از معادله زیر پیش‌بینی شود:

Y^ = θ1 + θ2X

یا

y^i = θ1 + θ2xi

در اینجا:

yiϵY (i=1,2,⋯ ,n) برچسب‌ها برای داده‌ها (یادگیری نظارت‌شده)
xiϵX (i=1,2,⋯ ,n) داده‌های ورودی مستقل آموزشی (یک متغیر – یک ویژگی)
yi^ϵY^ (i=1,2,⋯ ,n) مقادیر پیش‌بینی‌شده هستند.

مدل با پیدا کردن بهترین مقادیر θ1 و θ2 خط رگرسیون بهترین تطبیق را به‌دست می‌آورد.

θ1: عرض از مبدأ
θ2: ضریب x

پس از پیدا کردن بهترین مقادیر θ1 و θ2، خط بهترین تطبیق را خواهیم داشت. بنابراین، زمانی که مدل خود را برای پیش‌بینی استفاده می‌کنیم، مقدار y را برای مقدار ورودی x پیش‌بینی خواهد کرد.

چگونه مقادیر θ1 و θ2 را به‌روزرسانی کنیم تا بهترین خط تطبیق را به‌دست آوریم؟

برای دستیابی به خط رگرسیون بهترین تطبیق، مدل تلاش می‌کند تا مقدار هدف Y^ را پیش‌بینی کند به‌طوری‌که اختلاف خطا بین مقدار پیش‌بینی‌شده Y^ و مقدار واقعی Y به حداقل برسد. بنابراین، به‌روزرسانی مقادیر θ1 و θ2 بسیار مهم است تا به بهترین مقادیر برسیم که خطای بین مقدار پیش‌بینی‌شده y (pred) و مقدار واقعی y (y) را به حداقل برساند.

minimize 1/n ∑i=1n(yi^ − yi)²

انواع رگرسیون خطی

هنگامی که تنها یک ویژگی مستقل وجود داشته باشد، به آن رگرسیون خطی ساده یا رگرسیون خطی تک‌متغیره گفته می‌شود و زمانی که بیش از یک ویژگی وجود داشته باشد، به آن رگرسیون خطی چندگانه یا رگرسیون چندمتغیره گفته می‌شود.

رگرسیون خطی ساده

رگرسیون خطی ساده ساده‌ترین فرم رگرسیون خطی است و تنها شامل یک متغیر مستقل و یک متغیر وابسته می‌باشد. معادله رگرسیون خطی ساده به صورت زیر است: $y=β0+β1Xy = \beta_0 + \beta_1 X$ که در آن:

$YY$ متغیر وابسته است
$XX$ متغیر مستقل است
$β0\beta_0$ عرض از مبدا است
$β1\beta_1$ شیب خط است

فرضیات رگرسیون خطی ساده

رگرسیون خطی ابزاری قدرتمند برای درک و پیش‌بینی رفتار یک متغیر است، اما برای اینکه نتایج آن دقیق و قابل اعتماد باشند، باید چند شرط رعایت شود:

خطی بودن: بین متغیر مستقل و وابسته رابطه‌ای خطی وجود دارد. این به این معنی است که تغییرات در متغیر وابسته، به صورت خطی از تغییرات در متغیر مستقل پیروی می‌کند. به عبارت دیگر، باید یک خط مستقیم بتواند از نقاط داده عبور کند. اگر رابطه خطی نباشد، رگرسیون خطی مدل دقیقی نخواهد بود.

استقلال: مشاهدات موجود در مجموعه داده‌ها از یکدیگر مستقل هستند. به این معنی که مقدار متغیر وابسته برای یک مشاهده به مقدار متغیر وابسته برای مشاهده دیگری بستگی ندارد. اگر مشاهدات مستقل نباشند، رگرسیون خطی مدل دقیقی نخواهد بود.
همسان‌واریانس (Homoscedasticity): در تمامی سطوح متغیر مستقل، واریانس خطاها ثابت است. این نشان می‌دهد که مقدار متغیر مستقل تأثیری بر واریانس خطاها ندارد. اگر واریانس خطاها ثابت نباشد، رگرسیون خطی مدل دقیقی نخواهد بود.

نرمال بودن: باقی‌مانده‌ها باید به طور نرمال توزیع شوند. این به این معنی است که باقی‌مانده‌ها باید منحنی زنگی‌شکل (bell-shaped curve) را دنبال کنند. اگر باقی‌مانده‌ها نرمال توزیع نشوند، رگرسیون خطی مدل دقیقی نخواهد بود.

مورد استفاده رگرسیون خطی ساده

در یک مطالعه موردی که عملکرد دانش‌آموزان را ارزیابی می‌کند، تحلیلگران از رگرسیون خطی ساده برای بررسی رابطه بین ساعات مطالعه و نمرات امتحان استفاده می‌کنند. با جمع‌آوری داده‌ها در مورد تعداد ساعات مطالعه و نتایج امتحانات مربوطه، تحلیلگران مدلی توسعه می‌دهند که نشان می‌دهد برای هر ساعت اضافی که به مطالعه اختصاص داده می‌شود، نمرات امتحانی دانش‌آموزان به طور متوسط 5 امتیاز افزایش می‌یابد. این مطالعه نشان‌دهنده کارایی رگرسیون خطی ساده در درک و بهبود عملکرد تحصیلی است.
یک مطالعه موردی دیگر در زمینه بازاریابی و فروش است که در آن کسب‌وکارها از رگرسیون خطی ساده برای پیش‌بینی فروش بر اساس داده‌های تاریخی استفاده می‌کنند، به ویژه بررسی اینکه چگونه عواملی مانند هزینه‌های تبلیغاتی بر درآمد تأثیر می‌گذارد. با جمع‌آوری داده‌ها در مورد هزینه‌های تبلیغاتی گذشته و ارقام فروش مربوطه، تحلیلگران مدلی رگرسیونی توسعه می‌دهند که رابطه این متغیرها را نشان می‌دهد. به عنوان مثال، اگر تحلیل‌ها نشان دهند که برای هر دلار اضافی که برای تبلیغات خرج می‌شود، فروش به میزان 10 دلار افزایش می‌یابد، این قابلیت پیش‌بینی به شرکت‌ها کمک می‌کند تا استراتژی‌های تبلیغاتی خود را بهینه‌سازی کنند و منابع را به طور مؤثر تخصیص دهند.

رگرسیون خطی چندگانه

رگرسیون خطی چندگانه شامل بیش از یک متغیر مستقل و یک متغیر وابسته است. معادله رگرسیون خطی چندگانه به صورت زیر است: $y=β0+β1X1+β2X2+⋯+βnXny = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_n$ که در آن:

$YY$ متغیر وابسته است
$X1,X2,…,XnX_1, X_2, \dots, X_n$ متغیرهای مستقل هستند
$β0\beta_0$ عرض از مبدا است
$β1,β2,…,βn\beta_1, \beta_2, \dots, \beta_n$ شیب‌های خط هستند

هدف الگوریتم پیدا کردن بهترین معادله خط تطبیق است که می‌تواند مقادیر را بر اساس متغیرهای مستقل پیش‌بینی کند.

در رگرسیون، مجموعه‌ای از رکوردها با مقادیر $XX$ و $YY$ موجود است و از این مقادیر برای یادگیری یک تابع استفاده می‌شود تا اگر بخواهید $YY$ را از $XX$ ناشناخته پیش‌بینی کنید، از این تابع یادگرفته‌شده می‌توانید استفاده کنید. در رگرسیون باید مقدار $YY$ را پیدا کنیم، بنابراین تابعی نیاز است که $YY$ پیوسته را در حالت رگرسیون بر اساس $XX$ به عنوان ویژگی‌های مستقل پیش‌بینی کند.

فرضیات رگرسیون خطی چندگانه

برای رگرسیون خطی چندگانه، تمام چهار فرضیه از رگرسیون خطی ساده اعمال می‌شود. علاوه بر این، چند فرضیه دیگر نیز وجود دارد:

عدم هم‌خطی‌گذاری (Multicollinearity): هیچ همبستگی بالایی بین متغیرهای مستقل وجود ندارد. این نشان می‌دهد که بین متغیرهای مستقل همبستگی کمی یا هیچ همبستگی‌ای وجود ندارد. هم‌خطی‌گذاری زمانی رخ می‌دهد که دو یا بیشتر از متغیرهای مستقل به طور زیادی با یکدیگر همبسته باشند، که می‌تواند تعیین اثر فردی هر متغیر بر متغیر وابسته را دشوار کند. اگر هم‌خطی‌گذاری وجود داشته باشد، رگرسیون خطی چندگانه مدل دقیقی نخواهد بود.
افزایشی بودن: مدل فرض می‌کند که اثر تغییرات در یک متغیر پیش‌بینی‌کننده بر متغیر پاسخ ثابت است، صرف‌نظر از مقادیر سایر متغیرها. این فرضیه به این معنی است که هیچ تعاملی بین متغیرها در تأثیر آن‌ها بر متغیر وابسته وجود ندارد.
انتخاب ویژگی: در رگرسیون خطی چندگانه، انتخاب دقیق متغیرهای مستقل که در مدل وارد شوند، ضروری است. وارد کردن متغیرهای نامربوط یا اضافی ممکن است به بیش‌برازش (Overfitting) منجر شود و تفسیر مدل را پیچیده کند.
بیش‌برازش: بیش‌برازش زمانی رخ می‌دهد که مدل به داده‌های آموزشی بیش از حد تطبیق یابد و نویز یا نوسانات تصادفی را که نشان‌دهنده رابطه واقعی بین متغیرها نیست، در نظر بگیرد. این می‌تواند منجر به عملکرد ضعیف مدل بر روی داده‌های جدید و نادیده گرفته‌شده شود.

مورد استفاده رگرسیون خطی چندگانه

رگرسیون خطی چندگانه به ما این امکان را می‌دهد که رابطه بین چندین متغیر مستقل و یک متغیر وابسته را تحلیل کنیم. در اینجا چند مورد استفاده آورده شده است:

پیش‌بینی قیمت ملک: در املاک و مستغلات، رگرسیون خطی چندگانه برای پیش‌بینی قیمت ملک بر اساس عوامل مختلفی مانند موقعیت، اندازه، تعداد اتاق‌ها و غیره استفاده می‌شود. این به خریداران و فروشندگان کمک می‌کند تا روند بازار را درک کنند و قیمت‌های رقابتی تعیین کنند.
پیش‌بینی مالی: تحلیلگران مالی از رگرسیون خطی چندگانه برای پیش‌بینی قیمت سهام یا شاخص‌های اقتصادی بر اساس عوامل مختلف مانند نرخ بهره، نرخ تورم و روندهای بازار استفاده می‌کنند. این امر استراتژی‌های سرمایه‌گذاری و مدیریت ریسک بهتری را فراهم می‌آورد.
پیش‌بینی عملکرد کشاورزی: کشاورزان می‌توانند از رگرسیون خطی چندگانه برای تخمین عملکرد محصولات کشاورزی بر اساس چندین متغیر مانند بارش باران، دما، کیفیت خاک و استفاده از کود استفاده کنند. این اطلاعات در برنامه‌ریزی فعالیت‌های کشاورزی برای تولید بهینه کمک می‌کند.
تحلیل فروش در تجارت الکترونیک: یک شرکت تجارت الکترونیک می‌تواند از رگرسیون خطی چندگانه برای ارزیابی تأثیر عواملی مانند قیمت محصول، تبلیغات و روندهای فصلی بر فروش استفاده کند.

تابع هزینه برای رگرسیون خطی

همان‌طور که قبلاً در مورد خط بهترین برازش در رگرسیون خطی صحبت کردیم، در موارد واقعی بدست آوردن آن به راحتی امکان‌پذیر نیست، بنابراین باید خطاهایی که بر آن تأثیر می‌گذارند محاسبه شوند. این خطاها باید محاسبه شوند تا بتوان آنها را کاهش داد. تفاوت بین مقدار پیش‌بینی شده $Y^\hat{Y}$ و مقدار واقعی $YY$ تابع هزینه یا تابع زیان نامیده می‌شود.

در رگرسیون خطی، از تابع هزینه میانگین مربعات خطا (MSE) استفاده می‌شود که میانگین مربعات خطاها بین مقادیر پیش‌بینی شده $yi^\hat{y_i}$ و مقادیر واقعی $yiy_i$ را محاسبه می‌کند. هدف از این کار پیدا کردن مقادیر بهینه برای عرض از مبدا $θ1\theta_1$ و ضریب ویژگی ورودی $θ2\theta_2$ است که بهترین خط برازش برای داده‌های موجود را ارائه می‌دهد. معادله خطی که این رابطه را بیان می‌کند به صورت $yi^=θ1+θ2xi\hat{y_i} = \theta_1 + \theta_2 x_i$ است.

تابع MSE به صورت زیر محاسبه می‌شود:

$تابع هزینه(J)=1n∑i=1n(yi−yi^)2\text{تابع هزینه}(J) = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y_i})^2$

با استفاده از تابع MSE، فرایند تکراری نزول گرادیان برای به‌روزرسانی مقادیر $θ1\theta_1$ و $θ2\theta_2$ اعمال می‌شود. این فرایند باعث می‌شود که مقدار MSE به کمینه جهانی برسد که نشان‌دهنده بهترین برازش خط رگرسیون خطی به مجموعه داده‌ها است.

این فرایند شامل تنظیم مداوم پارامترهای $θ1\theta_1$ و $θ2\theta_2$ بر اساس گرادیان‌های محاسبه‌شده از MSE است. نتیجه نهایی یک خط رگرسیون خطی است که تفاوت‌های مربعی کلی بین مقادیر پیش‌بینی شده و واقعی را به حداقل می‌رساند و نمایشی بهینه از رابطه بنیادی در داده‌ها ارائه می‌دهد.

اکنون که تابع زیان را محاسبه کردیم، نیاز داریم که مدل را بهینه‌سازی کنیم تا این خطاها کاهش یابند و این کار از طریق نزول گرادیان انجام می‌شود.

نزول گرادیان برای رگرسیون خطی

مدل رگرسیون خطی می‌تواند با استفاده از الگوریتم بهینه‌سازی نزول گرادیان آموزش داده شود، که در آن پارامترهای مدل به طور تکراری برای کاهش میانگین مربعات خطا (MSE) مدل بر روی مجموعه داده آموزشی تغییر می‌کنند. برای به‌روزرسانی مقادیر $θ1\theta_1$ و $θ2\theta_2$ به‌منظور کاهش تابع هزینه (و کمینه‌سازی مقدار RMSE) و رسیدن به بهترین خط برازش، مدل از نزول گرادیان استفاده می‌کند. ایده این است که با مقادیر تصادفی شروع کرده و سپس به‌طور تکراری مقادیر را به‌روزرسانی کرده تا به کمینه هزینه برسیم.

یک گرادیان، در واقع مشتق است که تأثیرات ورودی‌های تابع را با تغییرات کوچک در ورودی‌ها تعریف می‌کند.

بیایید مشتق تابع هزینه $JJ$ را نسبت به $θ1\theta_1$ محاسبه کنیم:

$Jθ1′=∂J(θ1,θ2)∂θ1=∂∂θ1[1n∑i=1n(yi^−yi)2]=2n∑i=1n(yi^−yi)J’_{\theta_1} = \frac{\partial J(\theta_1, \theta_2)}{\partial \theta_1} = \frac{\partial}{\partial \theta_1} \left[ \frac{1}{n} \sum_{i=1}^{n} (\hat{y_i} – y_i)^2 \right] = \frac{2}{n} \sum_{i=1}^{n} (\hat{y_i} – y_i)$

حالا مشتق تابع هزینه $JJ$ را نسبت به $θ2\theta_2$ محاسبه می‌کنیم:

$Jθ2′=∂J(θ1,θ2)∂θ2=∂∂θ2[1n∑i=1n(yi^−yi)2]=2n∑i=1n(yi^−yi)⋅xiJ’_{\theta_2} = \frac{\partial J(\theta_1, \theta_2)}{\partial \theta_2} = \frac{\partial}{\partial \theta_2} \left[ \frac{1}{n} \sum_{i=1}^{n} (\hat{y_i} – y_i)^2 \right] = \frac{2}{n} \sum_{i=1}^{n} (\hat{y_i} – y_i) \cdot x_i$

برای به‌روزرسانی مقادیر $θ1\theta_1$ و $θ2\theta_2$ ، از فرمول‌های زیر استفاده می‌شود:

$θ1=θ1−α⋅Jθ1′\theta_1 = \theta_1 – \alpha \cdot J’_{\theta_1}$ $θ2=θ2−α⋅Jθ2′\theta_2 = \theta_2 – \alpha \cdot J’_{\theta_2}$

که در آن $α\alpha$ نرخ یادگیری است.

ارزیابی مدل رگرسیون خطی

برای ارزیابی قدرت مدل رگرسیون خطی از معیارهای مختلفی می‌توان استفاده کرد. این معیارها معمولاً نشان می‌دهند که مدل چگونه خروجی‌های مشاهده‌شده را تولید می‌کند.

مهم‌ترین معیارها عبارتند از:

میانگین مربعات خطا (MSE):
MSE یک معیار ارزیابی است که میانگین مربعات تفاوت‌ها بین مقادیر واقعی و پیش‌بینی‌شده برای تمام نقاط داده را محاسبه می‌کند. تفاوت‌ها مربع می‌شوند تا اطمینان حاصل شود که تفاوت‌های منفی و مثبت یکدیگر را خنثی نمی‌کنند.

فرمول MSE به صورت زیر است:

$MSE=1n∑i=1n(yi−yi^)2MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y_i})^2$
میانگین خطای مطلق (MAE):
MAE یک معیار ارزیابی است که دقت یک مدل رگرسیونی را محاسبه می‌کند. MAE میانگین تفاوت‌های مطلق بین مقادیر پیش‌بینی‌شده و واقعی را اندازه‌گیری می‌کند.

فرمول MAE به صورت زیر است:

$MAE=1n∑i=1n∣yi−yi^∣MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i – \hat{y_i}|$
ریشه میانگین مربعات خطا (RMSE):
RMSE، ریشه واریانس باقی‌مانده‌ها است و نشان‌دهنده چگونگی انطباق نقاط داده مشاهده‌شده با مقادیر پیش‌بینی‌شده یا برازش مدل به داده‌ها است.
ضریب تعیین (R-squared):
$R2R^2$ یک آمار است که نشان می‌دهد مدل چقدر از تغییرات متغیر وابسته را می‌تواند توضیح دهد یا آن را شبیه‌سازی کند. این معیار همیشه در بازه 0 تا 1 است. به طور کلی، هر چه مدل بهتر با داده‌ها تطابق داشته باشد، عدد $R2R^2$ بالاتر خواهد بود.
R-squared تعدیل‌شده:
R-squared تعدیل‌شده، بخشی از تغییرات متغیر وابسته را که توسط متغیرهای مستقل در مدل رگرسیون توضیح داده شده است اندازه‌گیری می‌کند. این معیار تعداد پیش‌بینی‌کننده‌ها را در مدل در نظر می‌گیرد و مدل را به دلیل استفاده از پیش‌بینی‌کننده‌های نامربوط جریمه می‌کند.

تکنیک‌های منظم‌سازی برای مدل‌های خطی

رگرسیون لاسو (L1 منظم‌سازی):
لاسو رگرسیون یک تکنیک برای منظم‌سازی مدل رگرسیون خطی است که یک عبارت جریمه به تابع هدف رگرسیون خطی اضافه می‌کند تا از پیچیدگی بیش از حد مدل جلوگیری کند.
رگرسیون ریج (L2 منظم‌سازی):
رگرسیون ریج یک تکنیک رگرسیون خطی است که یک عبارت جریمه اضافی به تابع هدف رگرسیون خطی اضافه می‌کند تا از پیچیدگی بیش از حد مدل جلوگیری کند.
رگرسیون شبکه الاستیک (Elastic Net):
رگرسیون شبکه الاستیک یک تکنیک منظم‌سازی ترکیبی است که قدرت هر دو L1 و L2 منظم‌سازی را در تابع هدف رگرسیون خطی ترکیب می‌کند.

پیاده‌سازی خطی رگرسیون در پایتون

وارد کردن کتابخانه‌های ضروری:
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.axes as ax
from matplotlib.animation import FuncAnimation
```
بارگذاری داده‌ها و جداسازی متغیر ورودی و هدف

در اینجا لینک داده‌ها: Dataset Link
```
url = 'https://media.geeksforgeeks.org/wp-content/uploads/20240320114716/data_for_lr.csv'
data = pd.read_csv(url)
data

# حذف مقادیر گمشده
data = data.dropna()

# مجموعه داده‌های آموزشی و برچسب‌ها
train_input = np.array(data.x[0:500]).reshape(500, 1)
train_output = np.array(data.y[0:500]).reshape(500, 1)

# مجموعه داده‌های تست و برچسب‌ها
test_input = np.array(data.x[500:700]).reshape(199, 1)
test_output = np.array(data.y[500:700]).reshape(199, 1)
```
ساخت مدل رگرسیون خطی و رسم خط رگرسیون

مراحل:
1. در پیش‌رفت رو به جلو، تابع رگرسیون خطی $Y=mx+cY = mx + c$ اعمال می‌شود که به طور تصادفی مقادیر پارامترها (m و c) اختصاص داده می‌شود.
2. سپس تابعی برای یافتن تابع هزینه یعنی میانگین مربع خطا نوشته می‌شود.
```
class LinearRegression:
    def __init__(self):
        self.parameters = {}

    def forward_propagation(self, train_input):
        m = self.parameters['m']
        c = self.parameters['c']
        predictions = np.multiply(m, train_input) + c
        return predictions

    def cost_function(self, predictions, train_output):
        cost = np.mean((train_output - predictions) ** 2)
        return cost

    def backward_propagation(self, train_input, train_output, predictions):
        derivatives = {}
        df = (predictions-train_output)
        # dm= 2/n * میانگین (پیش‌بینی‌ها - واقعی) * ورودی
        dm = 2 * np.mean(np.multiply(train_input, df))
        # dc = 2/n * میانگین (پیش‌بینی‌ها - واقعی)
        dc = 2 * np.mean(df)
        derivatives['dm'] = dm
        derivatives['dc'] = dc
        return derivatives

    def update_parameters(self, derivatives, learning_rate):
        self.parameters['m'] = self.parameters['m'] - learning_rate * derivatives['dm']
        self.parameters['c'] = self.parameters['c'] - learning_rate * derivatives['dc']

    def train(self, train_input, train_output, learning_rate, iters):
        # مقادیر تصادفی اولیه برای پارامترها
        self.parameters['m'] = np.random.uniform(0, 1) * -1
        self.parameters['c'] = np.random.uniform(0, 1) * -1

        # مقداردهی اولیه به ضرر
        self.loss = []

        # مقداردهی اولیه به نمودار و محورها برای انیمیشن
        fig, ax = plt.subplots()
        x_vals = np.linspace(min(train_input), max(train_input), 100)
        line, = ax.plot(x_vals, self.parameters['m'] * x_vals + self.parameters['c'], color='red', label='Regression Line')
        ax.scatter(train_input, train_output, marker='o', color='green', label='Training Data')

        # تعیین محدوده محور y برای جلوگیری از مقادیر منفی
        ax.set_ylim(0, max(train_output) + 1)

        def update(frame):
            # پیش‌رفت رو به جلو
            predictions = self.forward_propagation(train_input)

            # تابع هزینه
            cost = self.cost_function(predictions, train_output)

            # پس‌رفت
            derivatives = self.backward_propagation(train_input, train_output, predictions)

            # به‌روزرسانی پارامترها
            self.update_parameters(derivatives, learning_rate)

            # به‌روزرسانی خط رگرسیون
            line.set_ydata(self.parameters['m'] * x_vals + self.parameters['c'])

            # افزودن ضرر و چاپ آن
            self.loss.append(cost)
            print("Iteration = {}, Loss = {}".format(frame + 1, cost))

            return line,
        # ایجاد انیمیشن
        ani = FuncAnimation(fig, update, frames=iters, interval=200, blit=True)

        # ذخیره انیمیشن به عنوان فایل ویدئویی (مثلاً MP4)
        ani.save('linear_regression_A.gif', writer='ffmpeg')

        plt.xlabel('Input')
        plt.ylabel('Output')
        plt.title('Linear Regression')
        plt.legend()
        plt.show()

        return self.parameters, self.loss
```
آموزش مدل و پیش‌بینی نهایی
```
# مثال استفاده
linear_reg = LinearRegression()
parameters, loss = linear_reg.train(train_input, train_output, 0.0001, 20)
```
خروجی:
```
Iteration = 1, Loss = 9130.407560462196
Iteration = 1, Loss = 1107.1996742908998
Iteration = 1, Loss = 140.31580932842422
Iteration = 1, Loss = 23.795780526084116
Iteration = 2, Loss = 9.753848205147605
Iteration = 3, Loss = 8.061641745006835
Iteration = 4, Loss = 7.8577116490914864
Iteration = 5, Loss = 7.8331350515579015
Iteration = 6, Loss = 7.830172502503967
Iteration = 7, Loss = 7.829814681591015
Iteration = 8, Loss = 7.829770758846183
Iteration = 9, Loss = 7.829764664327399
Iteration = 10, Loss = 7.829763128602258
Iteration = 11, Loss = 7.829762142342088
Iteration = 12, Loss = 7.829761222379141
Iteration = 13, Loss = 7.829760310486438
Iteration = 14, Loss = 7.829759399646989
Iteration = 15, Loss = 7.829758489015161
Iteration = 16, Loss = 7.829757578489033
Iteration = 17, Loss = 7.829756668056319
Iteration = 18, Loss = 7.829755757715535
Iteration = 19, Loss = 7.829754847466484
Iteration = 20, Loss = 7.829753937309139
```
خط رگرسیون خطی نمایانگر رابطه‌ای است که بین دو متغیر وجود دارد. این خط بهترین تطبیق را برای نحوه تغییر یک متغیر وابسته (Y) در پاسخ به تغییرات یک متغیر مستقل (X) نشان می‌دهد.
- خط رگرسیون خطی مثبت: این خط نشان‌دهنده رابطه مستقیم بین متغیر مستقل (X) و وابسته (Y) است. به این معنا که وقتی مقدار X افزایش می‌یابد، مقدار Y نیز افزایش می‌یابد.
- خط رگرسیون خطی منفی: این خط نشان‌دهنده رابطه معکوس است. وقتی مقدار X افزایش می‌یابد، مقدار Y کاهش می‌یابد.
کاربردهای رگرسیون خطی

رگرسیون خطی در بسیاری از زمینه‌های مختلف از جمله مالی، اقتصاد و روان‌شناسی برای درک و پیش‌بینی رفتار یک متغیر خاص استفاده می‌شود.

برای مثال، رگرسیون خطی به طور گسترده‌ای در مالی برای تحلیل روابط و انجام پیش‌بینی‌ها استفاده می‌شود. این مدل می‌تواند تأثیر سود هر سهم (EPS) یک شرکت بر قیمت سهام آن را مدل‌سازی کند. اگر مدل نشان دهد که یک دلار افزایش در EPS باعث افزایش 15 دلار در قیمت سهام می‌شود، سرمایه‌گذاران می‌توانند بینش‌هایی در مورد ارزیابی شرکت کسب کنند. به طور مشابه، رگرسیون خطی می‌تواند با تحلیل نرخ‌های مبادله تاریخی و شاخص‌های اقتصادی، ارزش‌های ارزی را پیش‌بینی کند و به حرفه‌ای‌های مالی کمک می‌کند تا تصمیمات آگاهانه‌تری بگیرند و ریسک‌ها را به طور مؤثر مدیریت کنند.

مزایا و معایب رگرسیون خطی

مزایای رگرسیون خطی
- رگرسیون خطی یک الگوریتم نسبتاً ساده است که فهم و پیاده‌سازی آن راحت است. ضرایب مدل رگرسیون خطی می‌توانند به عنوان تغییرات در متغیر وابسته برای تغییر یک واحدی در متغیر مستقل تفسیر شوند و بینش‌هایی در مورد روابط بین متغیرها ارائه دهند.
- رگرسیون خطی از نظر محاسباتی کارآمد است و می‌تواند داده‌های بزرگ را به طور مؤثر پردازش کند. این مدل می‌تواند به سرعت بر روی داده‌های بزرگ آموزش ببیند و آن را برای کاربردهای بلادرنگ مناسب می‌سازد.
- رگرسیون خطی نسبت به الگوریتم‌های یادگیری ماشین دیگر نسبت به نقاط دورافتاده مقاوم‌تر است. نقاط دورافتاده ممکن است تأثیر کمتری بر عملکرد کلی مدل داشته باشند.
- رگرسیون خطی اغلب به عنوان یک مدل مبنایی خوب برای مقایسه با الگوریتم‌های پیچیده‌تر یادگیری ماشین عمل می‌کند.
- رگرسیون خطی یک الگوریتم تثبیت شده با تاریخچه غنی است و در کتابخانه‌ها و نرم‌افزارهای مختلف یادگیری ماشین به طور گسترده در دسترس است.
معایب رگرسیون خطی
- رگرسیون خطی فرض می‌کند که رابطه‌ای خطی بین متغیر وابسته و متغیرهای مستقل وجود دارد. اگر رابطه خطی نباشد، ممکن است مدل عملکرد خوبی نداشته باشد.
- رگرسیون خطی حساس به چندهمبستگی است، که زمانی رخ می‌دهد که همبستگی بالایی بین متغیرهای مستقل وجود داشته باشد. چندهمبستگی می‌تواند واریانس ضرایب را افزایش دهد و منجر به پیش‌بینی‌های ناپایدار مدل شود.
- رگرسیون خطی فرض می‌کند که ویژگی‌ها از قبل در فرم مناسبی برای مدل قرار دارند. ممکن است نیاز به مهندسی ویژگی‌ها باشد تا ویژگی‌ها به فرم مناسب برای مدل تبدیل شوند.
- رگرسیون خطی به شدت در معرض بیش‌برازش (Overfitting) و کم‌برازش (Underfitting) قرار دارد. بیش‌برازش زمانی اتفاق می‌افتد که مدل داده‌های آموزشی را به خوبی یاد می‌گیرد و قادر به تعمیم به داده‌های جدید نیست. کم‌برازش زمانی رخ می‌دهد که مدل خیلی ساده است و قادر به درک روابط نهفته در داده‌ها نیست.
- رگرسیون خطی توان توضیحی محدودی برای روابط پیچیده بین متغیرها دارد. برای بینش‌های عمیق‌تر ممکن است نیاز به تکنیک‌های پیشرفته‌تر یادگیری ماشین باشد.
نتیجه‌گیری

رگرسیون خطی یک الگوریتم بنیادی در یادگیری ماشین است که به دلیل سادگی، قابلیت تفسیر و کارآمدی آن برای سال‌ها به طور گسترده‌ای استفاده شده است. این مدل ابزاری ارزشمند برای درک روابط بین متغیرها و پیش‌بینی در انواع کاربردها است.

با این حال، مهم است که محدودیت‌های آن، مانند فرض خطی بودن رابطه و حساسیت به چندهمبستگی، در نظر گرفته شود. زمانی که این محدودیت‌ها به دقت مورد توجه قرار گیرند، رگرسیون خطی می‌تواند ابزار قدرتمندی برای تحلیل داده‌ها و پیش‌بینی باشد.

رگرسیون خطی – سوالات متداول

رگرسیون خطی به زبان ساده یعنی چه؟

رگرسیون خطی یک الگوریتم یادگیری ماشین نظارت‌شده است که یک متغیر هدف پیوسته را بر اساس یک یا چند متغیر مستقل پیش‌بینی می‌کند. این مدل فرض می‌کند که رابطه‌ای خطی بین متغیر وابسته و متغیرهای مستقل وجود دارد و از یک معادله خطی برای مدل‌سازی این رابطه استفاده می‌کند.

چرا از رگرسیون خطی استفاده می‌کنیم؟

رگرسیون خطی معمولاً برای موارد زیر استفاده می‌شود:
- پیش‌بینی مقادیر عددی بر اساس ویژگی‌های ورودی
- پیش‌بینی روندهای آینده بر اساس داده‌های تاریخی
- شناسایی همبستگی‌ها بین متغیرها
- درک تأثیر عوامل مختلف بر یک نتیجه خاص
چطور از رگرسیون خطی استفاده کنیم؟

برای استفاده از رگرسیون خطی، یک خط را برای پیش‌بینی رابطه بین متغیرها برازش کنید، ضرایب را درک کنید و پیش‌بینی‌هایی بر اساس مقادیر ورودی برای تصمیم‌گیری‌های آگاهانه انجام دهید.

چرا آن را رگرسیون خطی می‌نامند؟

رگرسیون خطی به دلیل استفاده از یک معادله خطی برای مدل‌سازی رابطه بین متغیرها نام‌گذاری شده است که یک خط مستقیم به داده‌ها برازش می‌دهد.

مثال‌هایی از رگرسیون خطی چیست؟

پیش‌بینی قیمت خانه‌ها بر اساس مساحت، برآورد نمرات امتحان از ساعات مطالعه و پیش‌بینی فروش با استفاده از هزینه‌های تبلیغات از جمله مثال‌های کاربرد رگرسیون خطی هستند.