تسلط بر حسابان برای یادگیری ماشین: مفاهیم کلیدی و کاربردها

حسابان یکی از دروس اساسی است که ارتباط نزدیکی با آموزش و یادگیری یادگیری ماشین (ML) دارد، زیرا پایه‌های ریاضی لازم برای فرمول‌های مورد استفاده در مدل‌ها را فراهم می‌کند. اگرچه حسابان برای همه وظایف یادگیری ماشین ضروری نیست، اما برای درک نحوه عملکرد مدل‌ها، تنظیم پارامترها و پیاده‌سازی برخی از تکنیک‌های پیشرفته ضروری است. این مقاله به بررسی حوزه‌های اصلی حسابان که در یادگیری ماشین کاربرد دارند، می‌پردازد تا به علاقه‌مندان در بهبود دانش خود کمک کند.

جدول محتوا

• درک نقش حسابان در یادگیری ماشین
• مفاهیم اساسی حسابان برای یادگیری ماشین
  ۱. مشتق‌گیری
  ۲. مشتقات جزئی
  ۳. گرادیان و کاهش گرادیان
  ۴. قاعده زنجیره‌ای
  ۵. ماتریس‌های ژاکوبین و هسیان
• کاربرد حسابان در الگوریتم‌های یادگیری ماشین
  ۱. رگرسیون خطی
  ۲. رگرسیون لجستیک
  ۳. شبکه‌های عصبی
  ۴. ماشین‌های بردار پشتیبان (SVMs)

درک نقش حسابان در یادگیری ماشین

حسابان یک ابزار اساسی در یادگیری ماشین است، به‌ویژه در توسعه الگوریتم‌ها و مدل‌ها. این ابزار چارچوب ریاضی برای درک نحوه یادگیری ماشین‌ها و بهینه‌سازی عملکرد آن‌ها فراهم می‌کند. حسابان برای توصیف پیشرفت یادگیری ماشین استفاده می‌شود و به متخصصان امکان تحلیل و بهبود فرآیند یادگیری را می‌دهد.

چرا حسابان در یادگیری ماشین مهم است؟

حسابان به‌دلیل ارائه ابزارهای لازم برای درک و بهینه‌سازی الگوریتم‌ها، بخشی جدایی‌ناپذیر از یادگیری ماشین است. به‌طور خاص، حسابان در موارد زیر کمک می‌کند:

• بهینه‌سازی: بسیاری از الگوریتم‌های یادگیری ماشین، مانند کاهش گرادیان، برای کمینه‌سازی یا بیشینه‌سازی یک تابع هزینه به حسابان متکی هستند. این شامل یافتن نقطه‌ای است که تابع به حداقل یا حداکثر مقدار خود می‌رسد، که برای آموزش مدل‌ها ضروری است.
• درک الگوریتم‌ها: حسابان به متخصصان امکان می‌دهد تا مکانیک زیربنایی الگوریتم‌ها را درک کنند. برای مثال، الگوریتم پس‌انتشار در شبکه‌های عصبی از مشتقات برای به‌روزرسانی وزن‌ها استفاده می‌کند.
• تقریب تابع: حسابان برای تقریب توابع استفاده می‌شود، که در سناریوهایی که راه‌حل‌های دقیق امکان‌پذیر نیستند، بسیار مهم است.

مفاهیم اساسی حسابان برای یادگیری ماشین

برای تمرین یادگیری ماشین، باید با چند مفهوم کلیدی در حسابان آشنا باشید:

۱. مشتق‌گیری

مشتق‌گیری فرآیند یافتن مشتق یک تابع است که میزان تغییرات خروجی تابع را نسبت به تغییرات ورودی آن اندازه‌گیری می‌کند. در یادگیری ماشین، مشتق‌گیری برای موارد زیر استفاده می‌شود:

• محاسبه گرادیان در الگوریتم‌های کاهش گرادیان.
• بهینه‌سازی توابع هزینه.
• درک حساسیت پیش‌بینی‌های مدل به تغییرات ورودی.

برای مثال، در کاهش گرادیان، مشتق تابع هزینه نسبت به پارامترهای مدل برای به‌روزرسانی تکراری پارامترها و کمینه‌سازی تابع هزینه استفاده می‌شود.

۲. مشتقات جزئی

مشتقات جزئی مفهوم مشتق‌گیری را به توابع چندمتغیره گسترش می‌دهند. آن‌ها میزان تغییرات تابع را هنگامی که یکی از متغیرهای ورودی تغییر می‌کند و سایر متغیرها ثابت نگه داشته می‌شوند، اندازه‌گیری می‌کنند. مشتقات جزئی در موارد زیر حیاتی هستند:

• مسائل بهینه‌سازی چندمتغیره.
• آموزش مدل‌هایی با چندین پارامتر، مانند شبکه‌های عصبی.

در شبکه‌های عصبی، مشتقات جزئی در الگوریتم پس‌انتشار برای محاسبه گرادیان تابع زیان نسبت به هر وزن استفاده می‌شوند.

۳. گرادیان و کاهش گرادیان

گرادیان یک بردار از مشتقات جزئی است و جهت بیشترین افزایش یک تابع را نشان می‌دهد. کاهش گرادیان یک الگوریتم بهینه‌سازی است که از گرادیان برای یافتن حداقل یک تابع استفاده می‌کند. این الگوریتم به‌طور گسترده در موارد زیر استفاده می‌شود:

• آموزش شبکه‌های عصبی.
• رگرسیون خطی و لجستیک.
• ماشین‌های بردار پشتیبان.

الگوریتم کاهش گرادیان به‌طور تکراری پارامترهای مدل را در جهت مخالف گرادیان تنظیم می‌کند تا تابع هزینه را کمینه کند.

۴. قاعده زنجیره‌ای

قاعده زنجیره‌ای فرمولی برای محاسبه مشتق یک تابع مرکب است. این قاعده در پس‌انتشار ضروری است، جایی که مشتق تابع زیان نسبت به هر وزن با زنجیره‌کردن مشتقات هر لایه در شبکه محاسبه می‌شود. این امر امکان محاسبه کارآمد گرادیان‌ها در مدل‌های یادگیری عمیق را فراهم می‌کند.

۵. ماتریس‌های ژاکوبین و هسیان

ماتریس ژاکوبین شامل تمام مشتقات جزئی مرتبه اول یک تابع برداری است، در حالی که ماتریس هسیان شامل تمام مشتقات جزئی مرتبه دوم است. این ماتریس‌ها در موارد زیر استفاده می‌شوند:

• تحلیل انحنای توابع هزینه.
• پیاده‌سازی تکنیک‌های بهینه‌سازی پیشرفته مانند روش نیوتن.

ماتریس ژاکوبین به‌ویژه برای درک چگونگی تأثیر تغییرات کوچک در متغیرهای ورودی بر بردار خروجی مفید است، که برای بهینه‌سازی چندمتغیره بسیار مهم است.

کاربرد حسابان در الگوریتم‌های یادگیری ماشین

۱. رگرسیون خطی

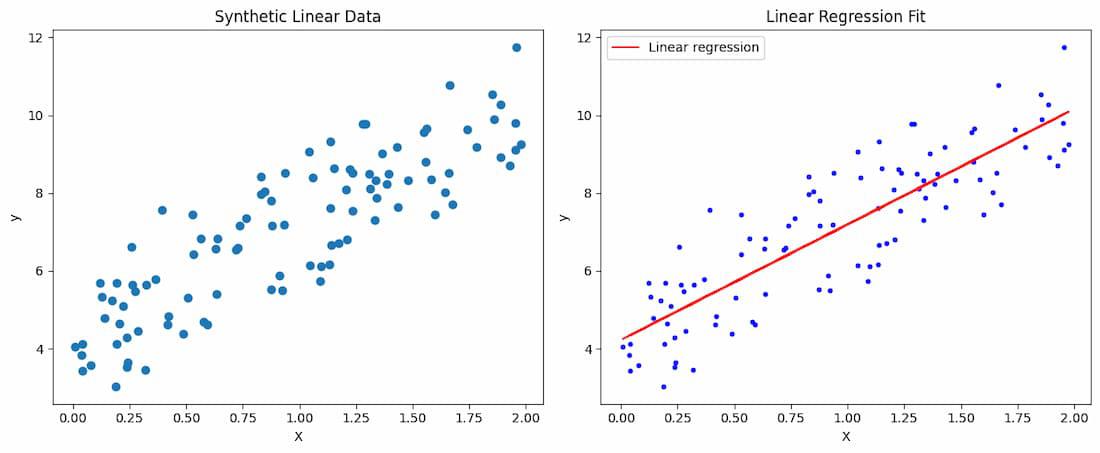
در رگرسیون خطی، حسابان برای استخراج معادلات نرمال برای راه‌حل کمترین مربعات استفاده می‌شود. تابع هزینه، معمولاً خطای میانگین مربعات، با استفاده از مشتق‌گیری کمینه می‌شود تا پارامترهای بهینه پیدا شوند.

این فرآیند شامل استفاده از مشتق‌گیری برای استخراج معادلات نرمال است. در ادامه، یک پیاده‌سازی عملی در پایتون برای نشان دادن چگونگی اعمال حسابان در رگرسیون خطی ارائه می‌شود

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# Add the bias term (x0 = 1) to each instance
X_b = np.c_[np.ones((100, 1)), X]

# Derive the Normal Equations Using Calculus
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print("Optimal parameters (theta):", theta_best)

fig, axs = plt.subplots(1, 2, figsize=(12, 5))

axs[0].scatter(X, y)
axs[0].set_title('Synthetic Linear Data')
axs[0].set_xlabel('X')
axs[0].set_ylabel('y')

# Plot 2: Linear regression fit
axs[1].plot(X, y, "b.")
axs[1].plot(X, X_b.dot(theta_best), "r-", label="Linear regression")
axs[1].set_title('Linear Regression Fit')
axs[1].set_xlabel('X')
axs[1].set_ylabel('y')
axs[1].legend()

plt.tight_layout()
plt.show()

خروجی

<pre>Optimal parameters (theta): [[4.22215108]
 [2.96846751]]

در این پیاده‌سازی، حسابان در مراحل زیر اعمال می‌شود:

1. تعریف تابع هزینه: خطای میانگین مربعات (MSE) نشان‌دهنده خطای بین مقادیر پیش‌بینی‌شده و مقادیر واقعی است.
2. محاسبه مشتق: با مشتق‌گیری از خطای میانگین مربعات (MSE) نسبت به پارامترها، مجموعه‌ای از معادلات خطی (معادلات نرمال) به دست می‌آید.
3. حل برای یافتن پارامترها: معادلات نرمال با استفاده از عملیات ماتریسی حل می‌شوند تا پارامترهای بهینه پیدا شوند.

این روش، که به عنوان معادله نرمال شناخته می‌شود، پارامترهای بهینه را مستقیماً و بدون نیاز به روش‌های تکراری مانند کاهش گرادیان محاسبه می‌کند. این یک کاربرد زیبا و کارآمد از حسابان در یادگیری ماشین است.

۲. رگرسیون لجستیک

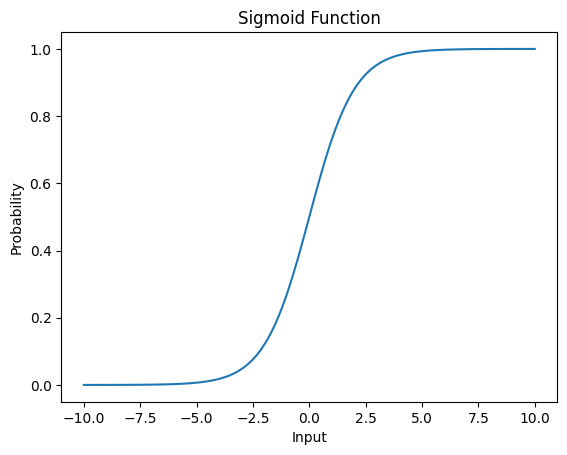
رگرسیون لجستیک از تابع سیگموئید برای مدل‌سازی احتمال یک نتیجه باینری استفاده می‌کند. تابع هزینه، که اغلب log-loss است، با استفاده از کاهش گرادیان کمینه می‌شود. این فرآیند نیاز به محاسبه گرادیان‌ها با استفاده از مشتقات دارد.

برای یافتن پارامترهای بهینه، گرادیان‌های تابع هزینه نسبت به پارامترهای مدل محاسبه می‌شوند و از کاهش گرادیان برای کمینه‌سازی تابع هزینه استفاده می‌شود.

در ادامه، یک پیاده‌سازی عملی از رگرسیون لجستیک ارائه می‌شود که کاربرد حسابان در یافتن پارامترهای بهینه را برجسته می‌کند:

<pre><span class="kn">import</span> <span class="nn">numpy</span> <span class="k">as</span> <span class="nn">np</span>
<span class="kn">import</span> <span class="nn">matplotlib.pyplot</span> <span class="k">as</span> <span class="nn">plt</span>

<span class="k">class</span> <span class="nc">LogisticRegression</span><span class="p">:</span>
    <span class="k">def</span> <span class="fm">__init__</span><span class="p">(</span><span class="bp">self</span><span class="p">,</span> <span class="n">learning_rate</span><span class="o">=</span><span class="mf">0.01</span><span class="p">,</span> <span class="n">n_iters</span><span class="o">=</span><span class="mi">1000</span><span class="p">):</span>
        <span class="bp">self</span><span class="o">.</span><span class="n">lr</span> <span class="o">=</span> <span class="n">learning_rate</span>
        <span class="bp">self</span><span class="o">.</span><span class="n">n_iters</span> <span class="o">=</span> <span class="n">n_iters</span>
        <span class="bp">self</span><span class="o">.</span><span class="n">weights</span> <span class="o">=</span> <span class="kc">None</span>
        <span class="bp">self</span><span class="o">.</span><span class="n">bias</span> <span class="o">=</span> <span class="kc">None</span>

    <span class="k">def</span> <span class="nf">fit</span><span class="p">(</span><span class="bp">self</span><span class="p">,</span> <span class="n">X</span><span class="p">,</span> <span class="n">y</span><span class="p">):</span>
        <span class="n">n_samples</span><span class="p">,</span> <span class="n">n_features</span> <span class="o">=</span> <span class="n">X</span><span class="o">.</span><span class="n">shape</span>

        <span class="c1"># Initialize parameters</span>
        <span class="bp">self</span><span class="o">.</span><span class="n">weights</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">zeros</span><span class="p">(</span><span class="n">n_features</span><span class="p">)</span>
        <span class="bp">self</span><span class="o">.</span><span class="n">bias</span> <span class="o">=</span> <span class="mi">0</span>

        <span class="c1"># Gradient descent</span>
        <span class="k">for</span> <span class="n">_</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="bp">self</span><span class="o">.</span><span class="n">n_iters</span><span class="p">):</span>
            <span class="n">linear_model</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">dot</span><span class="p">(</span><span class="n">X</span><span class="p">,</span> <span class="bp">self</span><span class="o">.</span><span class="n">weights</span><span class="p">)</span> <span class="o">+</span> <span class="bp">self</span><span class="o">.</span><span class="n">bias</span>
            <span class="n">y_predicted</span> <span class="o">=</span> <span class="bp">self</span><span class="o">.</span><span class="n">_sigmoid</span><span class="p">(</span><span class="n">linear_model</span><span class="p">)</span>
            <span class="c1"># Compute gradients</span>
            <span class="n">dw</span> <span class="o">=</span> <span class="p">(</span><span class="mi">1</span> <span class="o">/</span> <span class="n">n_samples</span><span class="p">)</span> <span class="o">*</span> <span class="n">np</span><span class="o">.</span><span class="n">dot</span><span class="p">(</span><span class="n">X</span><span class="o">.</span><span class="n">T</span><span class="p">,</span> <span class="p">(</span><span class="n">y_predicted</span> <span class="o">-</span> <span class="n">y</span><span class="p">))</span>
            <span class="n">db</span> <span class="o">=</span> <span class="p">(</span><span class="mi">1</span> <span class="o">/</span> <span class="n">n_samples</span><span class="p">)</span> <span class="o">*</span> <span class="n">np</span><span class="o">.</span><span class="n">sum</span><span class="p">(</span><span class="n">y_predicted</span> <span class="o">-</span> <span class="n">y</span><span class="p">)</span>

            <span class="c1"># Update parameters</span>
            <span class="bp">self</span><span class="o">.</span><span class="n">weights</span> <span class="o">-=</span> <span class="bp">self</span><span class="o">.</span><span class="n">lr</span> <span class="o">*</span> <span class="n">dw</span>
            <span class="bp">self</span><span class="o">.</span><span class="n">bias</span> <span class="o">-=</span> <span class="bp">self</span><span class="o">.</span><span class="n">lr</span> <span class="o">*</span> <span class="n">db</span>

    <span class="k">def</span> <span class="nf">predict</span><span class="p">(</span><span class="bp">self</span><span class="p">,</span> <span class="n">X</span><span class="p">):</span>
        <span class="n">linear_model</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">dot</span><span class="p">(</span><span class="n">X</span><span class="p">,</span> <span class="bp">self</span><span class="o">.</span><span class="n">weights</span><span class="p">)</span> <span class="o">+</span> <span class="bp">self</span><span class="o">.</span><span class="n">bias</span>
        <span class="n">y_predicted</span> <span class="o">=</span> <span class="bp">self</span><span class="o">.</span><span class="n">_sigmoid</span><span class="p">(</span><span class="n">linear_model</span><span class="p">)</span>
        <span class="n">y_predicted_cls</span> <span class="o">=</span> <span class="p">[</span><span class="mi">1</span> <span class="k">if</span> <span class="n">i</span> <span class="o">&gt;</span> <span class="mf">0.5</span> <span class="k">else</span> <span class="mi">0</span> <span class="k">for</span> <span class="n">i</span> <span class="ow">in</span> <span class="n">y_predicted</span><span class="p">]</span>
        <span class="k">return</span> <span class="n">y_predicted_cls</span>

    <span class="k">def</span> <span class="nf">_sigmoid</span><span class="p">(</span><span class="bp">self</span><span class="p">,</span> <span class="n">x</span><span class="p">):</span>
        <span class="k">return</span> <span class="mi">1</span> <span class="o">/</span> <span class="p">(</span><span class="mi">1</span> <span class="o">+</span> <span class="n">np</span><span class="o">.</span><span class="n">exp</span><span class="p">(</span><span class="o">-</span><span class="n">x</span><span class="p">))</span>

<span class="c1"># Example usage</span>
<span class="n">X</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">([[</span><span class="mi">0</span><span class="p">,</span> <span class="mi">0</span><span class="p">],</span> <span class="p">[</span><span class="mi">0</span><span class="p">,</span> <span class="mi">1</span><span class="p">],</span> <span class="p">[</span><span class="mi">1</span><span class="p">,</span> <span class="mi">0</span><span class="p">],</span> <span class="p">[</span><span class="mi">1</span><span class="p">,</span> <span class="mi">1</span><span class="p">]])</span>
<span class="n">y</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">([</span><span class="mi">0</span><span class="p">,</span> <span class="mi">1</span><span class="p">,</span> <span class="mi">1</span><span class="p">,</span> <span class="mi">0</span><span class="p">])</span>

<span class="n">model</span> <span class="o">=</span> <span class="n">LogisticRegression</span><span class="p">()</span>
<span class="n">model</span><span class="o">.</span><span class="n">fit</span><span class="p">(</span><span class="n">X</span><span class="p">,</span> <span class="n">y</span><span class="p">)</span>
<span class="n">predicted</span> <span class="o">=</span> <span class="n">model</span><span class="o">.</span><span class="n">predict</span><span class="p">(</span><span class="n">X</span><span class="p">)</span>
<span class="nb">print</span><span class="p">(</span><span class="n">predicted</span><span class="p">)</span>

<span class="n">x_values</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">linspace</span><span class="p">(</span><span class="o">-</span><span class="mi">10</span><span class="p">,</span> <span class="mi">10</span><span class="p">,</span> <span class="mi">100</span><span class="p">)</span>
<span class="n">y_values</span> <span class="o">=</span> <span class="p">[</span><span class="n">model</span><span class="o">.</span><span class="n">_sigmoid</span><span class="p">(</span><span class="n">i</span><span class="p">)</span> <span class="k">for</span> <span class="n">i</span> <span class="ow">in</span> <span class="n">x_values</span><span class="p">]</span>
<span class="n">plt</span><span class="o">.</span><span class="n">plot</span><span class="p">(</span><span class="n">x_values</span><span class="p">,</span> <span class="n">y_values</span><span class="p">)</span>
<span class="n">plt</span><span class="o">.</span><span class="n">xlabel</span><span class="p">(</span><span class="s1">'Input'</span><span class="p">)</span>
<span class="n">plt</span><span class="o">.</span><span class="n">ylabel</span><span class="p">(</span><span class="s1">'Probability'</span><span class="p">)</span>
<span class="n">plt</span><span class="o">.</span><span class="n">title</span><span class="p">(</span><span class="s1">'Sigmoid Function'</span><span class="p">)</span>
<span class="n">plt</span><span class="o">.</span><span class="n">show</span><span class="p">()</span></pre>

<pre>[0, 0, 0, 0]</pre>

در این پیاده‌سازی:

1. تابع سیگموئید: ترکیب خطی ورودی‌ها را به یک مقدار احتمال بین ۰ و ۱ تبدیل می‌کند.
2. تابع هزینه و کاهش گرادیان: تابع هزینه، یا log-loss، عملکرد مدل را اندازه‌گیری می‌کند. این تابع با استفاده از کاهش گرادیان کمینه می‌شود، که در آن پارامترهای مدل به‌صورت تکراری با محاسبه گرادیان‌ها به‌روزرسانی می‌شوند.
3. پیاده‌سازی کاهش گرادیان: در هر تکرار، گرادیان تابع هزینه نسبت به پارامترهای مدل محاسبه می‌شود و پارامترها بر این اساس به‌روزرسانی می‌شوند.
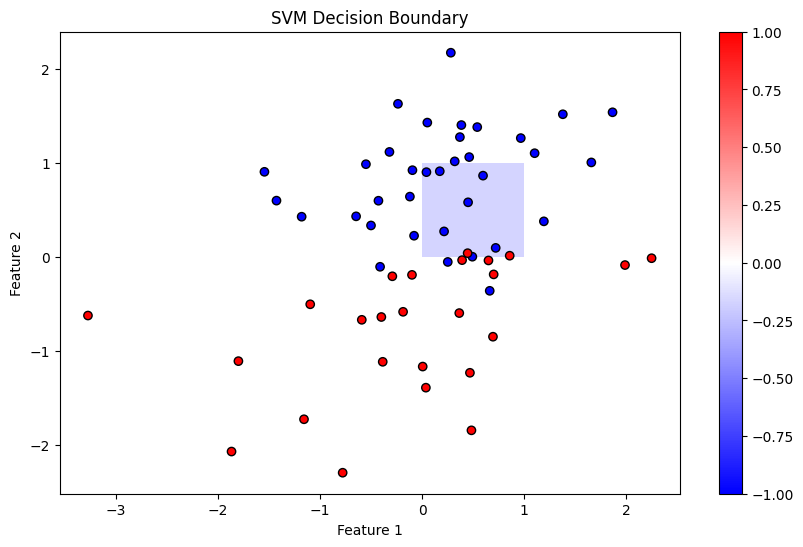
4. مرز تصمیم‌گیری: مرز تصمیم‌گیری با رسم خطی که در آن احتمال پیش‌بینی‌شده ۰.۵ است، تجسم می‌شود. این خط دو کلاس را از هم جدا می‌کند.

این کد نشان می‌دهد که چگونه حسابان، به‌ویژه مشتقات و کاهش گرادیان، در رگرسیون لجستیک برای یافتن پارامترهای بهینه جهت طبقه‌بندی نقاط داده اعمال می‌شود.

۳. شبکه‌های عصبی

شبکه‌های عصبی به‌طور گسترده از حسابان، به‌ویژه در الگوریتم پس‌انتشار (backpropagation)، استفاده می‌کنند. قاعده زنجیره‌ای برای محاسبه گرادیان تابع زیان نسبت به هر وزن استفاده می‌شود، که به‌روزرسانی کارآمد وزن‌ها در طول آموزش را امکان‌پذیر می‌سازد.

در ادامه، یک پیاده‌سازی عملی با استفاده از پایتون و TensorFlow/Keras ارائه می‌شود که نشان می‌دهد چگونه حسابان در شبکه‌های عصبی اعمال می‌شود

import numpy as np

# Define simple forward and backward functions for a single layer
def sigmoid(x):
return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))

# Example forward pass
def forward_pass(x, weights, bias):
return sigmoid(np.dot(x, weights) + bias)

# Example backward pass
def backward_pass(x, y, weights, bias, learning_rate):
output = forward_pass(x, weights, bias)
error = y - output
gradient = error * sigmoid_derivative(output)

print("Forward Pass Output:\n", output)
print("True Labels:\n", y)
print("Error:\n", error)
print("Gradient:\n", gradient)

# Update weights and bias
weights_update = learning_rate * np.dot(x.T, gradient)
bias_update = learning_rate * np.sum(gradient, axis=0)

weights += weights_update
bias += bias_update

# Print updated parameters
print("Weight Update:\n", weights_update)
print("Bias Update:\n", bias_update)
print("Updated Weights:\n", weights)
print("Updated Bias:\n", bias)

# Initialize parameters
weights = np.random.rand(784, 10)
bias = np.random.rand(10)
learning_rate = 0.01

# Example data
x_sample = np.random.rand(1, 784)
y_sample = np.random.rand(1, 10)

# Perform a single training step
backward_pass(x_sample, y_sample, weights, bias, learning_rate)

خروجی

<pre>Forward Pass Output:
 [[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]]
True Labels:
 [[0.35990872 0.7505352  0.79303902 0.3500513  0.43913699 0.44579077
  0.17421624 0.43067804 0.07465762 0.61567084]]
Error:
 [[-0.64009128 -0.2494648  -0.20696098 -0.6499487  -0.56086301 -0.55420923
  -0.82578376 -0.56932196 -0.92534238 -0.38432916]]
Gradient:
 [[-0.12584958 -0.04904776 -0.040691   -0.12778767 -0.11027236 -0.10896415
  -0.16235894 -0.11193549 -0.18193335 -0.0755637 ]]
Weight Update:
 [[-1.56831977e-04 -6.11226230e-05 -5.07085491e-05 ... -1.39492432e-04
  -2.26722780e-04 -9.41664173e-05]
 [-4.81740702e-05 -1.87750329e-05 -1.55761423e-05 ... -4.28478828e-05
  -6.96424243e-05 -2.89250934e-05]
 [-4.65633940e-04 -1.81472989e-04 -1.50553617e-04 ... -4.14152850e-04
  -6.73139643e-04 -2.79579972e-04]
 ...
 [-2.61773644e-04 -1.02021871e-04 -8.46393822e-05 ... -2.32831612e-04
  -3.78430785e-04 -1.57176404e-04]
 [-1.34838102e-05 -5.25508801e-06 -4.35972599e-06 ... -1.19930227e-05
  -1.94927525e-05 -8.09606634e-06]
 [-1.04744393e-04 -4.08223637e-05 -3.38670484e-05 ... -9.31637174e-05
  -1.51422818e-04 -6.28915375e-05]]
Bias Update:
 [-0.0012585  -0.00049048 -0.00040691 -0.00127788 -0.00110272 -0.00108964
 -0.00162359 -0.00111935 -0.00181933 -0.00075564]
Updated Weights:
 [[0.68060534 0.69338592 0.89135229 ... 0.12090908 0.84816228 0.54040066]
 [0.14948714 0.77843337 0.65844866 ... 0.99636285 0.20498507 0.99147941]
 [0.69210861 0.79538562 0.42402363 ... 0.12978548 0.01482275 0.85745295]
 ...
 [0.35523949 0.00989592 0.63079072 ... 0.17266939 0.08867039 0.32667996]
 [0.84543466 0.40684067 0.10459313 ... 0.78751296 0.92505182 0.21859855]
 [0.00517643 0.26806228 0.78420105 ... 0.49379695 0.74095303 0.44516112]]
Updated Bias:
 [0.33596314 0.16645184 0.39165508 0.11779942 0.43177188 0.33588123
 0.77762804 0.93207746 0.94497992 0.23917369]</pre>

در این پیاده‌سازی:

1. ابتدا یک شبکه عصبی ساده با استفاده از TensorFlow/Keras تنظیم می‌کنیم تا ارقام دست‌نوشته را از مجموعه‌داده MNIST طبقه‌بندی کند.
2. در شبکه‌های عصبی، تابع زیان اندازه‌گیری می‌کند که پیش‌بینی‌های مدل چقدر با برچسب‌های واقعی مطابقت دارند، در حالی که بهینه‌ساز وزن‌های مدل را بر اساس گرادیان‌ها تنظیم می‌کند.
3. در طول آموزش، الگوریتم پس‌انتشار از قاعده زنجیره‌ای برای محاسبه گرادیان تابع زیان نسبت به هر وزن استفاده می‌کند.
4. در الگوریتم پس‌انتشار، از حسابان برای محاسبه گرادیان‌ها استفاده می‌شود:
   • گذر به جلو (Forward Pass): خروجی شبکه محاسبه می‌شود.
   • گذر به عقب (Backward Pass): از قاعده زنجیره‌ای برای محاسبه گرادیان‌های تابع زیان نسبت به هر وزن استفاده می‌شود.

۴. ماشین‌های بردار پشتیبان (SVMs)

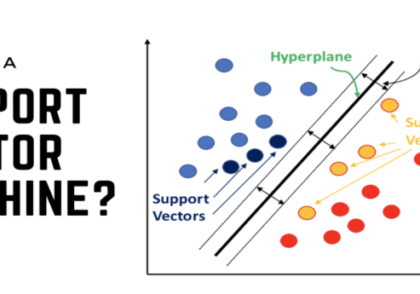
ماشین‌های بردار پشتیبان (SVMs) از حسابان برای استخراج ابرصفحه جداکننده بهینه با حداکثر کردن حاشیه بین کلاس‌های مختلف استفاده می‌کنند. این کار شامل حل یک مسئله بهینه‌سازی محدود با استفاده از تکنیک‌هایی مانند ضرب‌کننده‌های لاگرانژ است که نیاز به مشتقات جزئی دارد.

مراحل کلیدی در SVM:

1. فرموله‌کردن مسئله: تابع هدف و محدودیت‌ها را تعریف کنید.
2. اعمال حسابان: از ضرب‌کننده‌های لاگرانژ برای حل مسئله بهینه‌سازی محدود استفاده کنید.
3. پیاده‌سازی در پایتون: از کتابخانه‌هایی مانند Scikit-Learn برای انجام طبقه‌بندی SVM استفاده کنید.

در ادامه، یک پیاده‌سازی عملی از SVM با تمرکز بر کاربرد حسابان برای استخراج ابرصفحه بهینه ارائه می‌شود.

پیاده‌سازی عملی SVM در پایتون

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

np.random.seed(0)
X, y = datasets.make_classification(n_samples=200, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=1)
y = np.where(y == 0, -1, 1) # Convert to -1, 1 for SVM
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# Create an SVM classifier with a linear kernel
model = SVC(kernel=’linear’, C=1e-3) # Small C value for regularization
model.fit(X_train, y_train)

# Extract the coefficients
coef = model.coef_.flatten()
intercept = model.intercept_

# Step 3: Plot Decision Boundary
def plot_decision_boundary(X, y, model):
plt.figure(figsize=(10, 6))

# Plot decision boundary
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 100), np.linspace(ylim[0], ylim[1], 100))
Z = model.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, levels=[-1, 0, 1], colors=[‘#FFAAAA’, ‘#AAAAFF’, ‘#AAFFAA’], alpha=0.5, linestyles=[‘–‘, ‘-‘, ‘–‘])
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=’bwr’, edgecolor=’k’)
plt.title(‘SVM Decision Boundary’)
plt.xlabel(‘Feature 1’)
plt.ylabel(‘Feature 2’)
plt.colorbar()
plt.show()

plot_decision_boundary(X_test, y_test, model)

نتیجه‌گیری

درک حسابان برای تمرین مؤثر یادگیری ماشین ضروری است. مفاهیم کلیدی مانند مشتق‌گیری، مشتقات جزئی، کاهش گرادیان، قاعده زنجیره‌ای و ماتریس‌های ژاکوبین و هسیان، پایه‌های بسیاری از الگوریتم‌های یادگیری ماشین را تشکیل می‌دهند. با تسلط بر این مفاهیم، می‌توانید درک عمیق‌تری از نحوه عملکرد الگوریتم‌ها به دست آورید و آن‌ها را برای عملکرد بهتر بهینه‌سازی کنید.

سوالات متداول درباره حسابان برای یادگیری ماشین

۱. آیا قبل از شروع یادگیری ماشین باید بر حسابان مسلط شوم؟

• خیر، لازم نیست قبل از شروع یادگیری ماشین بر حسابان مسلط باشید، اما داشتن دانش پایه‌ای از حسابان بسیار مفید خواهد بود. با پیشرفت در یادگیری ماشین، این دانش بیشتر به کار می‌آید و باید گام‌های مربوطه را برداشت.

۲. مشتقات چقدر در یادگیری ماشین مهم هستند؟

• مشتقات به‌طور حیاتی در الگوریتم‌های بهینه‌سازی مانند کاهش گرادیان استفاده می‌شوند، که هسته اصلی آموزش مدل‌ها هستند.

۳. آیا می‌توانم فقط به کتابخانه‌های سطح بالا بدون درک حسابان تکیه کنم؟

• چارچوب‌هایی مانند TensorFlow و PyTorch بسیاری از محاسبات حسابان را پنهان می‌کنند، اما درک این مفاهیم به شما در رفع اشکال و تنظیم دقیق مدل‌هایتان کمک می‌کند.

۴. قاعده زنجیره‌ای در شبکه‌های عصبی چه نقشی دارد؟

• قاعده زنجیره‌ای در الگوریتم پس‌انتشار استفاده می‌شود و به شما امکان می‌دهد گرادیان‌ها را برای آموزش شبکه‌های عصبی عمیق محاسبه کنید.

۵. آیا انتگرال‌ها به‌طور مکرر در یادگیری ماشین استفاده می‌شوند؟

• انتگرال‌ها به اندازه مشتقات رایج نیستند، اما در مدل‌های احتمالی برای تعیین توزیع‌ها استفاده می‌شوند