درخت تصمیم در یادگیری ماشین

چرا از ساختار درخت تصمیم در یادگیری ماشین استفاده می‌کنیم؟

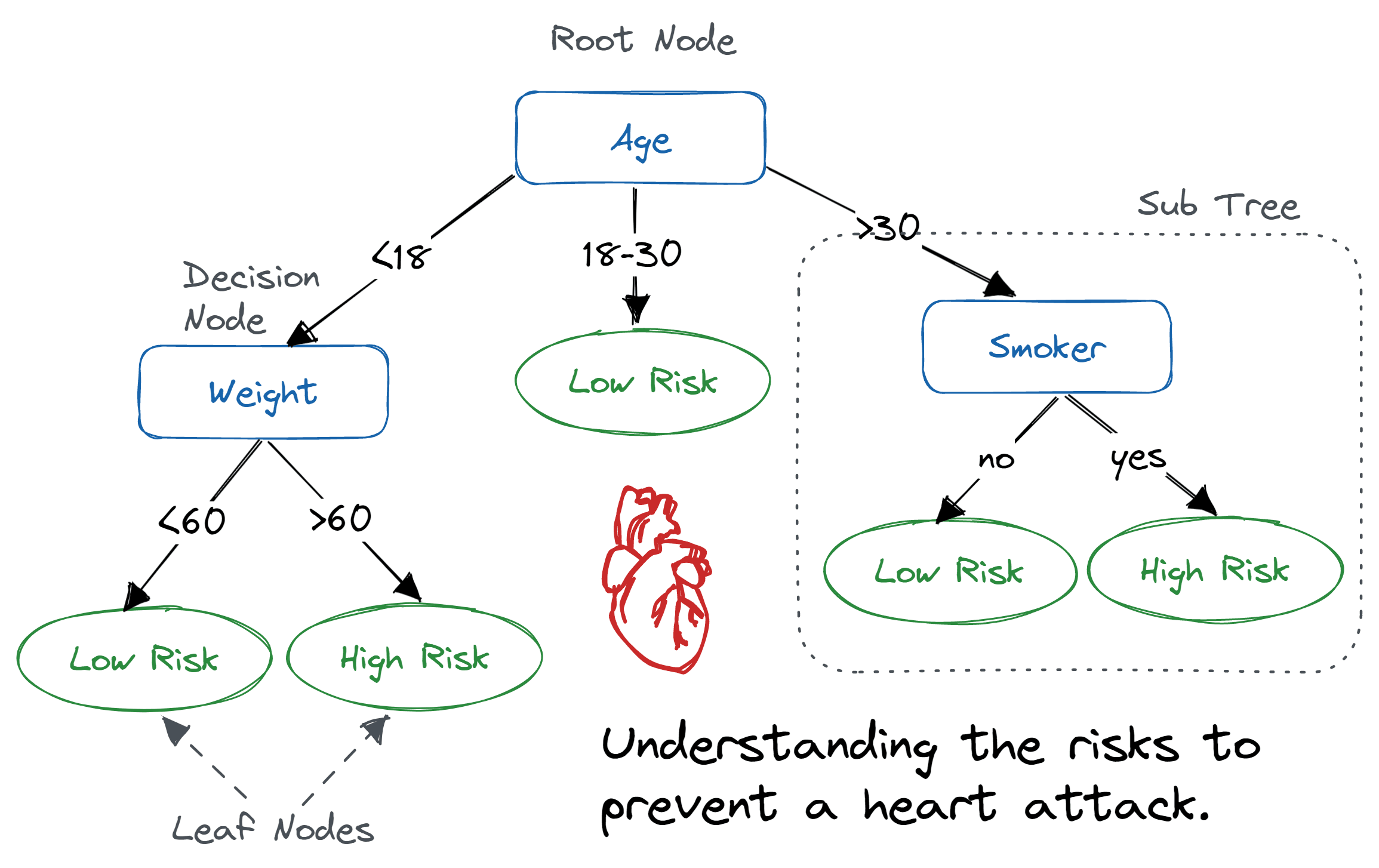
درخت تصمیم یک الگوریتم یادگیری نظارت‌شده است که برای هر دو وظیفه‌ی طبقه‌بندی و رگرسیون به کار می‌رود. این مدل تصمیمات را به‌صورت یک ساختار درختی نمایش می‌دهد، به‌طوری که:

گره‌های داخلی مشخص می‌کنند که چه ویژگی‌هایی باید بررسی شوند،
شاخه‌ها بیانگر مقادیر مختلف ویژگی‌ها هستند،
گره‌های برگ تصمیم نهایی یا پیش‌بینی را نشان می‌دهند.

درخت‌های تصمیم به دلیل سادگی، قابلیت تفسیر، و انعطاف‌پذیری بالا از محبوبیت زیادی در یادگیری ماشین برخوردارند.

شهود درخت تصمیم

برای درک بهتر نحوه‌ی کار درخت تصمیم، یک مثال ساده را در نظر بگیرید:

تصمیم‌گیری برای خرید چتر

مرحله اول – پرسیدن یک سؤال (گره ریشه)
- آیا باران می‌بارد؟
- اگر بله، چتر می‌خریم. اگر نه، به مرحله‌ی بعدی می‌رویم.
مرحله دوم – بررسی شرایط بیشتر (گره‌های داخلی)
- اگر باران نمی‌بارد، می‌پرسیم: آیا احتمال بارش باران در ادامه‌ی روز وجود دارد؟
- اگر بله، چتر می‌خریم؛ اگر نه، چتر نمی‌خریم.
مرحله سوم – تصمیم‌گیری نهایی (گره برگ)
- بر اساس پاسخ‌ها، یا چتر می‌خریم یا نمی‌خریم.

نحوه‌ی کار درخت تصمیم

درخت تصمیم از یک نمایش درختی برای حل مسائل استفاده می‌کند که در آن هر گره برگ نمایانگر یک برچسب کلاس و هر گره داخلی نمایانگر ویژگی‌های مسئله است. در واقع، هر تابع بولی که از ویژگی‌های گسسته استفاده کند را می‌توان با یک درخت تصمیم نمایش داد.

مثال: پیش‌بینی اینکه یک فرد به بازی‌های کامپیوتری علاقه دارد یا نه

فرض کنید می‌خواهیم پیش‌بینی کنیم که آیا یک شخص به بازی‌های کامپیوتری علاقه دارد یا نه، بر اساس سن و جنسیت.

شروع از گره ریشه (بررسی سن):
- آیا سن شخص کمتر از ۱۵ سال است؟
  - اگر بله → احتمال علاقه زیاد است (+۲ امتیاز).
  - اگر نه → به مرحله‌ی بعد می‌رویم.
بررسی جنسیت (برای افراد ۱۵ سال و بالاتر):
- آیا فرد مذکر است؟
  - اگر بله → احتمال علاقه متوسط (+0.1 امتیاز).
  - اگر نه → احتمال علاقه کم (-1 امتیاز).

ترکیب چندین درخت تصمیم

برای بهبود دقت پیش‌بینی، می‌توان چندین درخت تصمیم را با هم ترکیب کرد.

مثال: پیش‌بینی علاقه به بازی‌های کامپیوتری با استفاده از دو درخت تصمیم

✅ درخت ۱ (بررسی سن و جنسیت):

آیا سن فرد کمتر از ۱۵ سال است؟
- اگر بله → +۲ امتیاز.
- اگر نه → بررسی جنسیت:
  - اگر مذکر باشد → +۰.۱ امتیاز.
  - اگر مذکر نباشد → -۱ امتیاز.

✅ درخت ۲ (بررسی استفاده از کامپیوتر):

آیا فرد روزانه از کامپیوتر استفاده می‌کند؟
- اگر بله → +۰.۹ امتیاز.
- اگر نه → -۰.۹ امتیاز.

📌 جمع‌بندی: امتیاز نهایی مجموع امتیازات دو درخت است که مشخص می‌کند فرد چقدر احتمال دارد به بازی‌های کامپیوتری علاقه داشته باشد.

نتیجه‌گیری

درخت‌های تصمیم ابزار قدرتمندی برای طبقه‌بندی و پیش‌بینی هستند و می‌توانند با ترکیب شدن در قالب روش‌هایی مانند جنگل تصادفی (Random Forest) به دقت بیشتری دست یابند. این روش‌ها امروزه در بسیاری از کاربردهای هوش مصنوعی و علم داده مورد استفاده قرار می‌گیرند.

حاصل اطلاعات و شاخص جینی در درخت تصمیم

تا اینجا ما به پایه‌ای‌ترین درک و رویکرد درخت تصمیم پرداخته‌ایم، حالا بیایید به معیار انتخاب ویژگی‌ها در درخت تصمیم بپردازیم.

دو معیار انتخاب ویژگی محبوب برای استفاده در درخت‌های تصمیم وجود دارد:

حاصل اطلاعات (Information Gain)
شاخص جینی (Gini Index)

1. حاصل اطلاعات (Information Gain):

حاصل اطلاعات به ما می‌گوید که یک سوال (یا ویژگی) چقدر مفید است برای تقسیم داده‌ها به گروه‌ها. این معیار می‌سنجد که پس از تقسیم داده‌ها چقدر عدم اطمینان کاهش می‌یابد. سوال خوب، گروه‌ها را شفاف‌تر می‌کند و ویژگی‌ای که بیشترین حاصل اطلاعات را داشته باشد، برای گرفتن تصمیم انتخاب می‌شود.

برای مثال، اگر ما یک مجموعه داده از افراد را بر اساس سن به دو گروه “جوان” و “پیر” تقسیم کنیم، و تمام افراد جوان محصول را خریدند و تمام افراد پیر نخریدند، حاصل اطلاعات بالا خواهد بود چون تقسیم داده‌ها به طور کامل گروه‌ها را جدا کرده و هیچ عدم اطمینانی باقی نمی‌ماند.

فرض کنید S مجموعه‌ای از نمونه‌ها باشد، A ویژگی‌ای باشد که می‌خواهیم بر اساس آن تقسیم کنیم، Sv زیرمجموعه‌ای از S باشد که ویژگی A مقدار v را دارد و Values(A) مجموعه تمام مقادیر ممکن ویژگی A باشد، سپس

$Gain(S,A)=Entropy(S)−∑v(∣Sv∣∣S∣)⋅Entropy(Sv)\text{Gain}(S, A) = \text{Entropy}(S) – \sum_v \left( \frac{|S_v|}{|S|} \right) \cdot \text{Entropy}(S_v)$

انتروپی (Entropy): معیاری است برای اندازه‌گیری عدم اطمینان یک متغیر تصادفی و میزان اختلال در یک مجموعه نمونه‌ها. هرچه انتروپی بالاتر باشد، عدم اطمینان بیشتر است.

مثال:

برای مجموعه X = {a, a, a, b, b, b, b, b}
تعداد کل نمونه‌ها: 8
نمونه‌های b: 5
نمونه‌های a: 3

انتروپی H(X) برابر است با:

$H(X)=[38log⁡238+58log⁡258]=0.954H(X) = \left[ \frac{3}{8} \log_2 \frac{3}{8} + \frac{5}{8} \log_2 \frac{5}{8} \right] = 0.954$

ساخت درخت تصمیم با استفاده از حاصل اطلاعات:

مراحل اصلی عبارتند از:

با تمام نمونه‌های آموزشی در گره ریشه شروع کنید.
از حاصل اطلاعات برای انتخاب ویژگی‌ای که گره‌ها را بر اساس آن برچسب‌گذاری کنید، استفاده کنید.
از تقسیم مجدد هر زیرمجموعه برای ایجاد زیر درخت‌ها استفاده کنید.
اگر تمام نمونه‌ها مثبت یا تمام منفی باشند، برچسب گره “بله” یا “نه” خواهد بود.

2. شاخص جینی (Gini Index):

شاخص جینی معیاری است برای اندازه‌گیری اینکه یک عنصر به طور تصادفی از مجموعه داده به اشتباه شناسایی می‌شود. به عبارت دیگر، ویژگی با شاخص جینی پایین‌تر باید ترجیح داده شود.

برای مثال، اگر در گروهی از مردم همه محصول را خریدند (100% “بله”)، شاخص جینی برابر 0 خواهد بود، که نشان‌دهنده خلوص کامل است. اما اگر گروه ترکیبی از “بله” و “نه” باشد، شاخص جینی برابر 0.5 خواهد بود که نشان‌دهنده ناخالصی بیشتر است.

فرمول شاخص جینی به صورت زیر است:

$Gini=1−∑i=1npi2\text{Gini} = 1 – \sum_{i=1}^{n} p_i^2$

ویژگی‌های شاخص جینی:

شاخص جینی با جمع کردن مربعات احتمال‌های هر نتیجه در یک توزیع محاسبه می‌شود و نتیجه آن از 1 کم می‌شود.
هرچه شاخص جینی پایین‌تر باشد، توزیع همگن‌تر یا خالص‌تر است، در حالی که شاخص جینی بالاتر نشان‌دهنده توزیع ناهماهنگ‌تر است.
درخت‌های تصمیم برای ارزیابی کیفیت تقسیم‌ها از شاخص جینی استفاده می‌کنند، که تفاوت میان ناخالصی گره والد و ناخالصی وزنی گره‌های فرزند را اندازه‌گیری می‌کند.
یکی از معایب شاخص جینی این است که به تقسیم‌هایی تمایل دارد که گره‌های فرزند اندازه مشابهی داشته باشند، حتی اگر این تقسیم‌ها بهترین انتخاب برای دقت طبقه‌بندی نباشند.

مثال درخت تصمیم در دنیای واقعی:

مرحله 1: شروع با تمام داده‌ها
داده‌ها به عنوان گره ریشه در نظر گرفته می‌شوند.

مرحله 2: انتخاب بهترین سوال (ویژگی)
بهترین سوال برای تقسیم داده‌ها را انتخاب می‌کنیم. به عنوان مثال: “آیا وضعیت هوا آفتابی است؟”

مرحله 3: تقسیم داده‌ها به زیرمجموعه‌ها
داده‌ها را بر اساس جواب‌های سوال تقسیم می‌کنیم:

اگر آفتابی باشد، به زیرمجموعه اول می‌رویم.
اگر ابری باشد، به زیرمجموعه دوم می‌رویم.
اگر بارانی باشد، به زیرمجموعه سوم می‌رویم.

مرحله 4: تقسیم بیشتر در صورت نیاز (تقسیم بازگشتی)
برای هر زیرمجموعه، سوال دیگری می‌پرسیم تا گروه‌ها را دقیق‌تر کنیم.

مرحله 5: اختصاص تصمیمات نهایی (گره‌های برگ)
زمانی که یک زیرمجموعه تنها یک فعالیت را شامل می‌شود، تقسیم را متوقف کرده و برچسب می‌دهیم.

مرحله 6: استفاده از درخت برای پیش‌بینی
برای پیش‌بینی یک فعالیت، مسیر درخت را دنبال می‌کنیم.

نتیجه‌گیری:

درخت‌های تصمیم ابزارهای کلیدی در یادگیری ماشین هستند که از داده‌های ورودی برای مدل‌سازی و پیش‌بینی نتایج استفاده می‌کنند. آنها تفسیرپذیری، تطبیق‌پذیری و تصویری ساده برای نمایش فرآیندهای تصمیم‌گیری فراهم می‌کنند که آنها را برای انجام وظایف طبقه‌بندی و رگرسیون ارزشمند می‌سازد. با وجود مزایایی مانند سادگی درک، درخت‌های تصمیم ممکن است با مشکلاتی نظیر اورفیتینگ مواجه شوند. درک مفاهیم و مراحل تشکیل درخت‌های تصمیم برای کاربرد مؤثر آنها در سناریوهای مختلف ضروری است.

سوالات متداول (FAQ):

مسائل اصلی در یادگیری درخت تصمیم چیست؟ مشکلات اصلی در یادگیری درخت تصمیم شامل اورفیتینگ، حساسیت به تغییرات کوچک در داده‌ها و محدودیت در تعمیم‌پذیری است. اطمینان از هرس صحیح، تنظیم پارامترها و مدیریت داده‌های نامتعادل می‌تواند به کاهش این چالش‌ها کمک کند.
درخت تصمیم چگونه به تصمیم‌گیری کمک می‌کند؟ درخت‌های تصمیم با نمایش انتخاب‌های پیچیده در یک ساختار سلسله‌مراتبی کمک می‌کنند. هر گره ویژگی خاصی را بررسی می‌کند و با استفاده از مقادیر داده‌ها، تصمیم‌گیری را هدایت می‌کند.
حداکثر عمق درخت تصمیم چیست؟ عمق حداکثر درخت تصمیم یک ابرپارامتر است که تعیین می‌کند که تعداد لایه‌ها یا گره‌ها از ریشه تا هر برگ چقدر باشد.
مفهوم درخت تصمیم چیست؟ درخت تصمیم یک الگوریتم یادگیری نظارت‌شده است که بر اساس ویژگی‌های ورودی تصمیمات را مدل‌سازی می‌کند. این درخت به‌صورت یک ساختار درختی است که هر گره داخلی نمایانگر تصمیمی بر اساس ویژگی‌ها است.
انتروپی در درخت تصمیم چیست؟ در درخت‌های تصمیم، انتروپی معیاری برای اندازه‌گیری ناخالصی یا بی‌نظمی در یک مجموعه داده است که عدم اطمینان مرتبط با طبقه‌بندی نمونه‌ها را کم می‌کند.
ابرپارامترهای درخت تصمیم چیستند؟
- عمق حداکثر: عمق حداکثر درخت.
- حداقل نمونه‌های تقسیم: حداقل تعداد نمونه‌ها برای تقسیم یک گره داخلی.
- حداقل نمونه‌های برگ: حداقل تعداد نمونه‌ها در یک برگ.
- معیار: تابعی که برای اندازه‌گیری کیفیت تقسیم‌ها استفاده می‌شود.

درخت تصمیم در یادگیری ماشین