رگرسیون لجستیک در یادگیری ماشین

در بحث قبلی، اصول پایه‌ای یادگیری ماشین را بررسی کردیم و به پیاده‌سازی عملی رگرسیون خطی پرداختیم. حالا، بیایید یک قدم جلوتر برویم و به یکی از اولین و پرکاربردترین الگوریتم‌های طبقه‌بندی — رگرسیون لجستیک بپردازیم.

رگرسیون لجستیک چیست؟

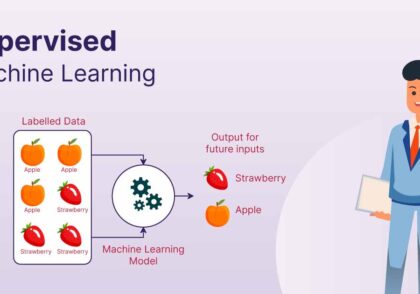
رگرسیون لجستیک یک الگوریتم یادگیری ماشین نظارت‌شده است که برای وظایف طبقه‌بندی استفاده می‌شود، جایی که هدف پیش‌بینی احتمال تعلق یک نمونه به یک کلاس خاص است یا نه. رگرسیون لجستیک یک الگوریتم آماری است که رابطه بین دو عامل داده را تجزیه و تحلیل می‌کند. این مقاله به اصول پایه‌ای رگرسیون لجستیک، انواع آن و پیاده‌سازی‌های آن می‌پردازد.

رگرسیون لجستیک برای طبقه‌بندی دوتایی استفاده می‌شود که در آن از تابع سیگموید استفاده می‌شود، که ورودی‌ها را به عنوان متغیرهای مستقل می‌گیرد و یک مقدار احتمالی بین 0 و 1 تولید می‌کند.

به عنوان مثال، اگر دو کلاس Class 0 و Class 1 داشته باشیم، اگر مقدار تابع لجستیک برای یک ورودی بیشتر از 0.5 (مقدار آستانه) باشد، به Class 1 تعلق دارد وگرنه به Class 0 تعلق دارد. به آن رگرسیون گفته می‌شود چون گسترشی از رگرسیون خطی است، اما عمدتاً برای مسائل طبقه‌بندی استفاده می‌شود.

نکات کلیدی:

رگرسیون لجستیک پیش‌بینی‌کننده خروجی یک متغیر وابسته دسته‌ای است. بنابراین، نتیجه باید یک مقدار دسته‌ای یا گسسته باشد.
این می‌تواند بله یا خیر، 0 یا 1، درست یا غلط و غیره باشد، اما به جای دادن مقدار دقیق به 0 و 1، مقادیر احتمالی بین 0 و 1 را می‌دهد.
در رگرسیون لجستیک، به جای تطبیق یک خط رگرسیونی، یک تابع لجستیک به شکل “S” را تطبیق می‌دهیم که دو مقدار حداکثر (0 یا 1) را پیش‌بینی می‌کند.

انواع رگرسیون لجستیک

بر اساس دسته‌ها، رگرسیون لجستیک می‌تواند به سه نوع تقسیم شود:

دوتایی: در رگرسیون لجستیک دوتایی، تنها دو نوع ممکن از متغیر وابسته وجود دارد، مانند 0 یا 1، قبولی یا مردودی و غیره.
چندگانه: در رگرسیون لجستیک چندگانه، سه یا بیشتر نوع نامرتب ممکن از متغیر وابسته وجود دارد، مانند “گربه”، “سگ” یا “گوسفند”.
ترتیبی: در رگرسیون لجستیک ترتیبی، سه یا بیشتر نوع مرتب ممکن از متغیرهای وابسته وجود دارد، مانند “کم”، “متوسط” یا “بالا”.

فرضیات رگرسیون لجستیک

ما فرضیات رگرسیون لجستیک را بررسی خواهیم کرد، زیرا درک این فرضیات برای اطمینان از استفاده مناسب از مدل ضروری است. فرضیات شامل موارد زیر است:

مشاهدات مستقل: هر مشاهده مستقل از دیگری است، به این معنی که هیچ همبستگی بین متغیرهای ورودی وجود ندارد.
متغیرهای وابسته دوتایی: این فرضیه می‌گوید که متغیر وابسته باید دوتایی یا دوگانه باشد، به این معنی که فقط دو مقدار می‌تواند داشته باشد. برای بیش از دو دسته از توابع SoftMax استفاده می‌شود.
رابطه خطی بین متغیرهای مستقل و لگاریتم شانس‌ها: رابطه بین متغیرهای مستقل و لگاریتم شانس‌های متغیر وابسته باید خطی باشد.
عدم وجود مقادیر پرت: در مجموعه داده‌ها نباید مقادیر پرت وجود داشته باشد.
اندازه نمونه بزرگ: اندازه نمونه به اندازه کافی بزرگ است.

درک تابع سیگموید

تا اینجا، اصول پایه‌ای رگرسیون لجستیک را بررسی کردیم، اما حالا بیایید روی مهم‌ترین تابعی که هسته رگرسیون لجستیک را تشکیل می‌دهد تمرکز کنیم.

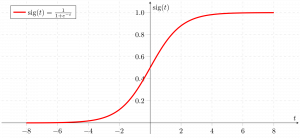
تابع سیگموید یک تابع ریاضی است که برای نگاشت مقادیر پیش‌بینی‌شده به احتمالات استفاده می‌شود.
این تابع هر مقدار واقعی را به یک مقدار دیگر در بازه 0 و 1 نگاشت می‌کند. مقدار رگرسیون لجستیک باید بین 0 و 1 باشد، که نمی‌تواند از این حد فراتر رود، بنابراین یک منحنی به شکل “S” ایجاد می‌کند.
منحنی به شکل “S” به نام تابع سیگموید یا تابع لجستیک شناخته می‌شود.
در رگرسیون لجستیک، از مفهوم مقدار آستانه استفاده می‌کنیم که احتمال 0 یا 1 را تعریف می‌کند. به عنوان مثال، مقادیر بالاتر از مقدار آستانه به سمت 1 میل می‌کنند و مقادیر پایین‌تر از مقدار آستانه به سمت 0 میل می‌کنند.

رگرسیون لجستیک چگونه کار می‌کند؟

مدل رگرسیون لجستیک، خروجی مقدار پیوسته تابع رگرسیون خطی را به خروجی مقدار دسته‌ای با استفاده از تابع سیگموید تبدیل می‌کند که هر مجموعه از متغیرهای مستقل ورودی را به یک مقدار بین 0 و 1 نگاشت می‌کند. این تابع به نام تابع لجستیک شناخته می‌شود.

فرض کنید ویژگی‌های ورودی مستقل به صورت زیر هستند:

X = [x₁₁ … x₁m; x₂₁ … x₂m; ⋮; xn₁ … xnm]

و متغیر وابسته Y تنها مقدار دوتایی دارد، یعنی 0 یا 1.

Y = {0 اگر Class 1 باشد؛ 1 اگر Class 2 باشد}

سپس، تابع چندگانه را به متغیرهای ورودی X اعمال می‌کنیم.

z = (Σᵢ=1ⁿ wᵢ xᵢ) + b

در اینجا xᵢ مشاهدات i‌ام از X است، wᵢ = [w₁, w₂, w₃, ⋯, wm] وزن‌ها یا ضرایب هستند، و b عبارت تعصب است که به آن تقاطع نیز گفته می‌شود. به سادگی این را می‌توان به صورت ضرب داخلی وزن و تعصب نمایش داد.

z = w ⋅ X + b

تمامی آنچه که در بالا بحث کردیم، رگرسیون خطی است.

معادله رگرسیون لجستیک:

اُد (Odds) نسبت وقوع یک رویداد به عدم وقوع آن است. این از احتمال متفاوت است زیرا احتمال نسبت وقوع یک رویداد به تمام وقایعی است که ممکن است رخ دهند. بنابراین اُد به شکل زیر خواهد بود:

$p(x)1−p(x)=ez\frac{p(x)}{1-p(x)} = e^{z}$

با اعمال لگاریتم طبیعی بر روی اُد، لگ اُد به صورت زیر خواهد بود:

$log⁡(p(x)1−p(x))=z\log \left( \frac{p(x)}{1-p(x)} \right) = z$

که در آن $z=w⋅X+bz = w \cdot X + b$ است. این معادله مشابه رگرسیون خطی است.

سپس معادله نهایی رگرسیون لجستیک به صورت زیر خواهد بود:

$p(X;b,w)=ew⋅X+b1+ew⋅X+bp(X; b, w) = \frac{e^{w \cdot X + b}}{1 + e^{w \cdot X + b}}$

تابع likelihood برای رگرسیون لجستیک:

احتمالات پیش‌بینی شده به صورت زیر خواهند بود:

برای $y=1y = 1$ احتمال پیش‌بینی شده: $p(X;b,w)=p(x)p(X; b, w) = p(x)$
برای $y=0y = 0$ احتمال پیش‌بینی شده: $1-p(X;b,w)=1-p(x)1 - p(X; b, w) = 1 - p(x)$

تابع likelihood به صورت زیر خواهد بود:

$L(b,w)=∏i=1np(xi)yi(1−p(xi))1−yiL(b, w) = \prod_{i=1}^{n} p(x_i)^{y_i} (1 – p(x_i))^{1 – y_i}$

با اعمال لگاریتم طبیعی بر هر دو طرف معادله:

$log⁡(L(b,w))=∑i=1nyilog⁡p(xi)+(1−yi)log⁡(1−p(xi))\log(L(b, w)) = \sum_{i=1}^{n} y_i \log p(x_i) + (1 – y_i) \log (1 – p(x_i))$ $=∑i=1nlog⁡(1−p(xi))+∑i=1nyilog⁡p(xi)= \sum_{i=1}^{n} \log(1 – p(x_i)) + \sum_{i=1}^{n} y_i \log p(x_i)$

برای پیدا کردن بیشینه‌های likelihood، مشتق این تابع نسبت به $ww$ به صورت زیر خواهد بود:

$∂J(L(b,w))∂wj=−∑i=1n11+ew⋅xi+bxij+∑i=1nyixij\frac{\partial J(L(b, w))}{\partial w_j} = – \sum_{i=1}^{n} \frac{1}{1 + e^{w \cdot x_i + b}} x_{ij} + \sum_{i=1}^{n} y_i x_{ij}$

این مشتق را می‌توان به صورت زیر نوشت:

$=∑i=1n(yi−p(xi;b,w))xij= \sum_{i=1}^{n} (y_i – p(x_i; b, w)) x_{ij}$

اصطلاحات مرتبط با رگرسیون لجستیک:

در اینجا برخی اصطلاحات رایج در رگرسیون لجستیک آورده شده است:

متغیرهای مستقل: ویژگی‌ها یا عوامل پیش‌بینی‌کننده ورودی که برای پیش‌بینی متغیر وابسته استفاده می‌شوند.
متغیر وابسته: متغیر هدف در مدل رگرسیون لجستیک که سعی داریم آن را پیش‌بینی کنیم.
تابع لجستیک: فرمولی که نشان می‌دهد چگونه متغیرهای مستقل و وابسته به یکدیگر مرتبط هستند. تابع لجستیک ورودی‌ها را به یک مقدار احتمال بین 0 و 1 تبدیل می‌کند که احتمال این که متغیر وابسته برابر 1 یا 0 باشد را نشان می‌دهد.
اُد: نسبت وقوع یک رویداد به عدم وقوع آن. این با احتمال متفاوت است زیرا احتمال نسبت وقوع یک رویداد به تمام وقایعی است که ممکن است رخ دهند.
لگ اُد: لگ اُد یا تابع لاگیت، لگاریتم طبیعی اُد است. در رگرسیون لجستیک، لگ اُد متغیر وابسته به صورت یک ترکیب خطی از متغیرهای مستقل و عرض از مبدأ مدل می‌شود.
ضریب: پارامترهای تخمینی مدل رگرسیون لجستیک که نشان می‌دهند متغیرهای مستقل و وابسته چگونه به یکدیگر مرتبط هستند.
عرض از مبدأ: یک عبارت ثابت در مدل رگرسیون لجستیک که نمایانگر لگ اُد زمانی است که تمام متغیرهای مستقل برابر صفر باشند.
برآورد حداکثر احتمال: روشی که برای تخمین ضرایب مدل رگرسیون لجستیک استفاده می‌شود که احتمال مشاهده داده‌ها را در شرایط مدل بیشینه می‌کند.

پیاده‌سازی کد برای رگرسیون لجستیک:

تا به اینجا، مفاهیم اساسی رگرسیون لجستیک را با تمام مفاهیم تئوری پوشش داده‌ایم، اما اکنون بیایید به بخش پیاده‌سازی کد بپردازیم که به شما کمک می‌کند رگرسیون لجستیک را بهتر درک کنید. ابتدا رگرسیون لجستیک دوتایی (Binomial Logistic Regression) و سپس رگرسیون لجستیک چندگانه (Multinomial Logistic Regression) را بررسی خواهیم کرد.

رگرسیون لجستیک دوتایی:

متغیر هدف می‌تواند تنها دو نوع ممکن داشته باشد: “0” یا “1”، که ممکن است نمایانگر “برد” در برابر “باخت”، “قبول” در برابر “رد”، “زنده” در برابر “مرده” و غیره باشد. در این حالت، از توابع سیگموید استفاده می‌شود که قبلاً توضیح داده شد.

وارد کردن کتابخانه‌های مورد نیاز بر اساس نیاز مدل. این کد پایتون نشان می‌دهد که چگونه از دیتاست سرطان سینه برای پیاده‌سازی مدل رگرسیون لجستیک جهت دسته‌بندی استفاده کنیم.

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# بارگذاری دیتاست سرطان سینه
X, y = load_breast_cancer(return_X_y=True)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23)

clf = LogisticRegression(max_iter=10000, random_state=0)
clf.fit(X_train, y_train)

acc = accuracy_score(y_test, clf.predict(X_test)) * 100
print(f"دقت مدل رگرسیون لجستیک: {acc:.2f}%")

خروجی:

دقت مدل رگرسیون لجستیک (به درصد): 96.49%

این کد دیتاست سرطان سینه را از کتابخانه scikit-learn بارگذاری می‌کند، آن را به مجموعه‌های آموزشی و آزمایشی تقسیم می‌کند و سپس مدل رگرسیون لجستیک را بر روی داده‌های آموزشی آموزش می‌دهد. مدل برای پیش‌بینی برچسب‌ها برای داده‌های آزمایشی استفاده می‌شود و دقت این پیش‌بینی‌ها با مقایسه مقادیر پیش‌بینی‌شده با برچسب‌های واقعی از مجموعه آزمایشی محاسبه می‌شود. در نهایت، دقت به صورت درصدی چاپ می‌شود.

رگرسیون لجستیک چندکلاسه:

متغیر هدف می‌تواند سه یا بیشتر نوع ممکن داشته باشد که ترتیب‌پذیر نیستند (یعنی انواع هیچ‌گونه معنای کمی ندارند) مانند “بیماری A” در مقابل “بیماری B” در مقابل “بیماری C”.

در این حالت، از تابع softmax به جای تابع سیگموید استفاده می‌شود. تابع softmax برای K کلاس به صورت زیر است:

softmax(zi) = ezi / ∑(j=1 to K) ezj

در اینجا، K نمایانگر تعداد عناصر در بردار z است و i و j بر روی تمام عناصر بردار تکرار می‌شوند.

سپس احتمال کلاس c به صورت زیر خواهد بود:

P(Y=c | X=x) = (ewc⋅x + bc) / ∑(k=1 to K) (ewk⋅x + bk)

در رگرسیون لجستیک چندکلاسه، متغیر خروجی می‌تواند بیش از دو خروجی گسسته ممکن داشته باشد. به عنوان مثال، دیتاست ارقام را در نظر بگیرید.

from sklearn.model_selection import train_test_split
from sklearn import datasets, linear_model, metrics

digits = datasets.load_digits()

X = digits.data
y = digits.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)

reg = linear_model.LogisticRegression(max_iter=10000, random_state=0)
reg.fit(X_train, y_train)

y_pred = reg.predict(X_test)

print(f"دقت مدل رگرسیون لجستیک: {metrics.accuracy_score(y_test, y_pred) * 100:.2f}%")

خروجی:

دقت مدل رگرسیون لجستیک (به درصد): 96.66%

چگونه مدل رگرسیون لجستیک را ارزیابی کنیم؟

تا اینجا، پیاده‌سازی رگرسیون لجستیک را پوشش دادیم. حالا بیایید به ارزیابی مدل رگرسیون لجستیک بپردازیم و بفهمیم که چرا این کار مهم است.

ارزیابی مدل به ما کمک می‌کند تا عملکرد مدل را ارزیابی کرده و اطمینان حاصل کنیم که مدل به خوبی به داده‌های جدید تعمیم می‌یابد.

ما می‌توانیم مدل رگرسیون لجستیک را با استفاده از معیارهای زیر ارزیابی کنیم:

دقت (Accuracy): دقت میزان نمونه‌های دسته‌بندی شده درست را ارائه می‌دهد.
```
دقت = (True Positives + True Negatives) / Total
```
دقت (Precision): دقت بر دقت پیش‌بینی‌های مثبت تمرکز دارد.
```
دقت = True Positives / (True Positives + False Positives)
```
بازخوانی (Recall یا نرخ مثبت واقعی): بازخوانی میزان نمونه‌های مثبت پیش‌بینی شده درست را در بین تمام نمونه‌های مثبت واقعی اندازه‌گیری می‌کند.
```
بازخوانی = True Positives / (True Positives + False Negatives)
```
امتیاز F1: امتیاز F1 میانگین هارمونیک دقت و بازخوانی است.
```
امتیاز F1 = 2 * (دقت * بازخوانی) / (دقت + بازخوانی)
```
مساحت زیر منحنی ویژگی‌های گیرنده (AUC-ROC): منحنی ROC نرخ مثبت واقعی را در مقابل نرخ مثبت کاذب در آستانه‌های مختلف ترسیم می‌کند. AUC-ROC مساحت زیر این منحنی را اندازه‌گیری می‌کند و یک معیار کلی از عملکرد مدل در آستانه‌های مختلف دسته‌بندی ارائه می‌دهد.
مساحت زیر منحنی دقت-بازخوانی (AUC-PR): مشابه AUC-ROC، AUC-PR مساحت زیر منحنی دقت-بازخوانی را اندازه‌گیری می‌کند و یک خلاصه از عملکرد مدل در تعادل‌های مختلف دقت-بازخوانی ارائه می‌دهد.

تفاوت‌های بین رگرسیون خطی و رگرسیون لجستیک

حال به تفاوت‌های کلیدی بین رگرسیون خطی و رگرسیون لجستیک می‌پردازیم و بررسی می‌کنیم که چگونه این دو از یکدیگر متفاوت هستند.

تفاوت بین رگرسیون خطی و رگرسیون لجستیک این است که خروجی رگرسیون خطی یک مقدار پیوسته است که می‌تواند هر مقداری باشد، در حالی که رگرسیون لجستیک احتمال تعلق یک نمونه به یک کلاس خاص را پیش‌بینی می‌کند.

رگرسیون خطی

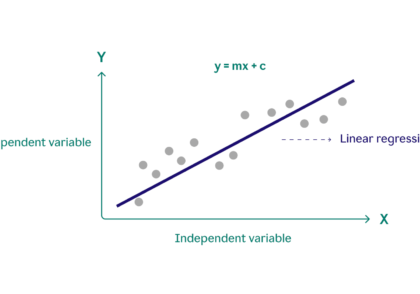
رگرسیون خطی برای پیش‌بینی متغیر وابسته پیوسته با استفاده از مجموعه‌ای از متغیرهای مستقل استفاده می‌شود.
در رگرسیون خطی، برای حل مسائل رگرسیون استفاده می‌شود.
در اینجا ما مقدار متغیرهای پیوسته مانند قیمت، سن و غیره را پیش‌بینی می‌کنیم.
در اینجا خط بهترین برازش پیدا می‌شود.