الگوریتم ماشین بردار پشتیبان (SVM)

الگوریتم ماشین بردار پشتیبان (SVM)

آخرین بروزرسانی: ۲۷ ژانویه ۲۰۲۵

ماشین بردار پشتیبان (SVM) یک الگوریتم یادگیری ماشین نظارتی است که برای طبقه‌بندی و رگرسیون استفاده می‌شود. با اینکه SVM می‌تواند مسائل رگرسیونی را حل کند، اما بیشتر برای مسائل طبقه‌بندی مناسب است.

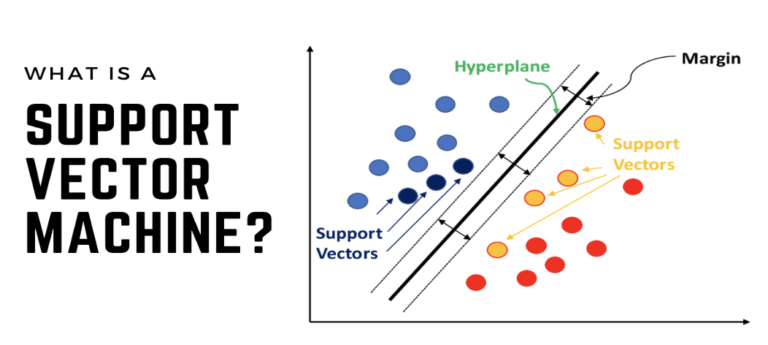
این الگوریتم سعی می‌کند بهینه‌ترین ابرصفحه (Hyperplane) را در یک فضای N بعدی پیدا کند تا داده‌ها را به درستی از هم جدا کند. هدف اصلی آن، حداکثر کردن فاصله (Margin) بین نزدیک‌ترین نقاط داده از دو کلاس مختلف است.

اصطلاحات کلیدی در SVM

• ابرصفحه (Hyperplane): یک مرز تصمیم‌گیری که کلاس‌های مختلف را از هم جدا می‌کند. در طبقه‌بندی خطی، با معادله wx + b = 0 نمایش داده می‌شود.
• بردارهای پشتیبان (Support Vectors): نزدیک‌ترین نقاط داده به ابرصفحه، که تعیین‌کننده‌ی محل ابرصفحه و میزان فاصله آن هستند.
• فاصله (Margin): فاصله بین ابرصفحه و بردارهای پشتیبان. SVM این فاصله را حداکثر می‌کند تا دقت طبقه‌بندی افزایش یابد.
• کرنل (Kernel): تابعی که داده‌ها را به یک فضای با بعد بالاتر نگاشت می‌کند تا SVM بتواند داده‌های غیرخطی را طبقه‌بندی کند.
• فاصله سخت (Hard Margin): حالتی که ابرصفحه بدون هیچ خطایی داده‌ها را از هم جدا می‌کند.
• فاصله نرم (Soft Margin): اجازه می‌دهد برخی از داده‌ها اشتباه طبقه‌بندی شوند تا مدل تعمیم بهتری داشته باشد.
• C (پارامتر تنظیم‌کننده): عاملی که تعادل بین حداکثر کردن فاصله و جریمه‌ی اشتباهات طبقه‌بندی را کنترل می‌کند. مقدار C بالاتر به معنای جریمه سخت‌تر برای خطاها است.
• تابع هزینه Hinge Loss: جریمه‌ای که برای نقاطی که به‌درستی طبقه‌بندی نشده‌اند یا باعث نقض فاصله شده‌اند اعمال می‌شود.
• مسئله دوگان (Dual Problem): یک رویکرد ریاضی که محاسبات را بهینه می‌کند و باعث می‌شود ترفند کرنل (Kernel Trick) در SVM عملی شود.

نحوه کار الگوریتم SVM

ایده اصلی این است که ابرصفحه‌ای را پیدا کند که داده‌های دو کلاس را بهترین شکل ممکن از هم جدا کند. این ابرصفحه حداکثر فاصله ممکن را از نزدیک‌ترین نقاط هر کلاس (بردارهای پشتیبان) خواهد داشت.

انتخاب بهترین ابرصفحه:
تصور کنید که چندین ابرصفحه برای جدا کردن دو کلاس وجود دارد. اما الگوریتم SVM آن ابرصفحه‌ای را انتخاب می‌کند که بیشترین فاصله را از بردارهای پشتیبان داشته باشد.

داده‌های دارای نویز و تأثیر آنها

گاهی در مجموعه داده‌ها نقاط پرت (Outliers) وجود دارند که ممکن است باعث تغییر محل ابرصفحه شوند. اما SVM این توانایی را دارد که با استفاده از فاصله نرم (Soft Margin)، برخی داده‌های نویزی را نادیده بگیرد و بهترین ابرصفحه را پیدا کند.

تابع هدف SVM:
الگوریتم SVM به دنبال حل معادله زیر است که تعادلی بین حداکثر کردن فاصله و مینیمم کردن جریمه اشتباهات برقرار می‌کند:

Objective Function=(1−margin)+λ∑penalty\text{Objective Function} = (1 – \text{margin}) + \lambda \sum \text{penalty}

در این فرمول:

• اگر داده به درستی طبقه‌بندی شده باشد، جریمه صفر است.
• اگر داده به اشتباه طبقه‌بندی شده باشد یا فاصله را نقض کند، تابع هزینه‌ی Hinge Loss افزایش پیدا می‌کند.

چگونه با داده‌های غیرخطی کار کنیم؟

تا اینجا، فقط درباره داده‌های خطی صحبت کردیم (یعنی داده‌هایی که می‌توان با یک خط مستقیم از هم جدا کرد). اما در بسیاری از موارد، داده‌ها غیرخطی هستند و با یک خط مستقیم نمی‌توان آنها را جدا کرد.

راه‌حل:
برای حل این مشکل، SVM از کرنل‌ها (Kernels) استفاده می‌کند که داده‌ها را به یک فضای با بعد بالاتر نگاشت می‌کند، جایی که در آن قابل جداسازی باشند.

انواع کرنل‌ها

• کرنل خطی (Linear Kernel): برای داده‌های خطی مناسب است.
• کرنل چندجمله‌ای (Polynomial Kernel): داده‌ها را به فضای چندجمله‌ای می‌برد.
• کرنل تابع پایه شعاعی (RBF – Radial Basis Function): براساس فاصله بین داده‌ها، آنها را به یک فضای جدید تبدیل می‌کند.

مثال:
فرض کنید داده‌های شما در یک بعدی قرار دارند و جداپذیر نیستند. با استفاده از یک کرنل مناسب، می‌توان آنها را به یک فضای دوبعدی یا سه‌بعدی برد، جایی که کاملاً از هم جدا شوند

ماشین بردار پشتیبان (SVM) – محاسبات ریاضی و پیاده‌سازی

مسئله دسته‌بندی دودویی
در مسئله دسته‌بندی دودویی، دو کلاس وجود دارند که با برچسب‌های +1 و -1 نشان داده می‌شوند. مجموعه داده آموزشی شامل بردارهای ویژگی X و برچسب‌های مربوطه Y است.

معادله ابرصفحه (Hyperplane) خطی

معادله ابرصفحه (مرز تصمیم‌گیری) به صورت زیر تعریف می‌شود:

wTx+b=0w^T x + b = 0

که در آن:

• ww بردار نرمال به ابرصفحه است (جهتی که بر ابرصفحه عمود است).
• bb مقدار بایاس یا افست است که فاصله ابرصفحه از مبدأ را نشان می‌دهد.

فاصله یک نقطه داده از ابرصفحه تصمیم‌گیری

فاصله یک نقطه xix_i از ابرصفحه به صورت زیر محاسبه می‌شود:

di=wTxi+b∥w∥d_i = \frac{w^T x_i + b}{\|w\|}

که در آن ∥w∥\|w\| نُرم اقلیدسی بردار وزن ww است.

طبقه‌بندی‌کننده خطی SVM

تابع تصمیم‌گیری در ماشین بردار پشتیبان به صورت زیر است:

y^={1,اگر wTx+b≥00,اگر wTx+b<0\hat{y} = \begin{cases} 1, & \text{اگر } w^T x + b \geq 0 \\ 0, & \text{اگر } w^T x + b < 0 \end{cases}

که در آن y^\hat{y} برچسب پیش‌بینی‌شده برای نمونه داده است.

مسئله بهینه‌سازی در SVM

هدف از SVM خطی این است که ابرصفحه‌ای پیدا شود که حاشیه (margin) را بیشینه کند و داده‌ها را به درستی طبقه‌بندی کند. این مسئله به صورت زیر بیان می‌شود:

min⁡w,b12∥w∥2\min_{w,b} \quad \frac{1}{2} \|w\|^2

شرط قیود:

yi(wTxi+b)≥1,∀i=1,2,…,my_i (w^T x_i + b) \geq 1, \quad \forall i = 1,2,\dots, m

که در آن:

• yiy_i برچسب کلاس (+1 یا -1) برای هر نمونه آموزشی است.
• xix_i بردار ویژگی هر نمونه است.
• mm تعداد نمونه‌های آموزشی است.

SVM با حاشیه نرم (Soft Margin SVM)

در صورت وجود نویز یا داده‌های غیرقابل تفکیک خطی، از متغیرهای کمکی (ζi\zeta_i) استفاده می‌شود تا اجازه داده شود برخی داده‌ها به درون حاشیه نفوذ کنند:

min⁡w,b12∥w∥2+C∑i=1mζi\min_{w,b} \quad \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{m} \zeta_i

شرایط قیود:

yi(wTxi+b)≥1−ζi,ζi≥0,∀i=1,2,…,my_i (w^T x_i + b) \geq 1 – \zeta_i, \quad \zeta_i \geq 0, \quad \forall i = 1,2,\dots,m

که در آن CC یک پارامتر تنظیمی است که بین افزایش حاشیه و مجازات نمونه‌های نادرست طبقه‌بندی شده تعادل برقرار می‌کند.

مسئله دوگان (Dual Form) در SVM

در فرم دوگان، مسئله به جای بردارهای وزن ww، روی ضرایب لاگرانژ (α\alpha) حل می‌شود:

max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjK(xi,xj)\max_{\alpha} \quad \sum_{i=1}^{m} \alpha_i – \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j K(x_i, x_j)

که در آن:

• αi\alpha_i ضرایب لاگرانژ برای هر نمونه است.
• K(xi,xj)K(x_i, x_j) تابع کرنل برای مقایسه داده‌ها است.

انواع ماشین بردار پشتیبان

✅ SVM خطی: برای داده‌هایی که با یک ابرصفحه خطی قابل تفکیک هستند.
✅ SVM غیرخطی: از توابع کرنل برای تبدیل داده‌ها به فضای بعد بالاتر استفاده می‌کند و مرزهای غیرخطی ایجاد می‌کند.

پیاده‌سازی SVM در پایتون

مدلی برای تشخیص سرطان (خوش‌خیم یا بدخیم) بر اساس داده‌های بیماران با استفاده از SVM و کرنل RBF پیاده‌سازی می‌کنیم:

# بارگذاری پکیج‌های لازم
from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.svm import SVC

# بارگذاری دیتاست سرطان سینه
cancer = load_breast_cancer()
X = cancer.data[:, :2]  # انتخاب دو ویژگی اول برای نمایش دو بعدی
y = cancer.target       # برچسب‌ها (خوش‌خیم یا بدخیم)

# ساخت مدل SVM با کرنل RBF
svm = SVC(kernel="rbf", gamma=0.5, C=1.0)
svm.fit(X, y)  # آموزش مدل

# نمایش مرز تصمیم‌گیری
DecisionBoundaryDisplay.from_estimator(
    svm, X, response_method="predict",
    cmap=plt.cm.Spectral, alpha=0.8,
    xlabel=cancer.feature_names[0], ylabel=cancer.feature_names[1]
)

# نمایش نقاط داده
plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolors="k")
plt.show()

📌 خروجی:
نموداری که مرز تصمیم‌گیری بین نمونه‌های سرطان خوش‌خیم و بدخیم را نمایش می‌دهد.

مزایای ماشین بردار پشتیبان (SVM)

✅ کارایی بالا در فضاهای با بعد بالا (مانند پردازش تصویر و ژنتیک).
✅ توانایی مدل‌سازی روابط غیرخطی با استفاده از کرنل‌ها.
✅ مقاوم در برابر داده‌های پرت با استفاده از حاشیه نرم.
✅ مناسب برای مسائل دسته‌بندی دودویی و چندکلاسه.
✅ مدل‌های بهینه و حافظه‌ای کم‌مصرف چون فقط از بردارهای پشتیبان استفاده می‌کند.

معایب ماشین بردار پشتیبان (SVM)

❌ سرعت پایین در دیتاست‌های بزرگ (هزینه محاسباتی بالا).
❌ نیاز به تنظیم دقیق پارامترها (مانند C و نوع کرنل).
❌ حساسیت به نویز و داده‌های هم‌پوشان.
❌ تفسیر سخت در فضاهای بعد بالا.
❌ نیاز به نرمال‌سازی ویژگی‌ها برای عملکرد بهتر.

سؤالات متداول درباره SVM

1. ماشین بردار پشتیبان چگونه کار می‌کند؟
SVM یک ابرصفحه بهینه را پیدا می‌کند که بیشترین فاصله را از نقاط داده دو کلاس دارد. داده‌های نزدیک به این ابرصفحه بردارهای پشتیبان نامیده می‌شوند.

2. تفاوت بین SVM حاشیه سخت و نرم چیست؟

• حاشیه سخت (Hard Margin): کلاس‌ها را بدون هیچ خطایی از هم جدا می‌کند.
• حاشیه نرم (Soft Margin): اجازه برخی خطاها را می‌دهد تا به نویز حساس نباشد.

3. چه زمانی از SVM استفاده کنیم؟
✅ وقتی که داده‌ها دارای ابعاد بالا هستند.
✅ زمانی که به دقت بالا نیاز داریم و سرعت آموزش مهم نیست.
✅ در مسائل غیرخطی که استفاده از کرنل‌ها باعث بهبود عملکرد می‌شود.